Гомотетія з центром \(O\) і коефіцієнтом \(k\) — це перетворення, в якому кожна точка \(P\) відображається такою точкою \(.\)
Гомотетія — це перетворення подібності. Це перетворення, в якому виходять подібні фігури (фігури, в яких відповідні кути рівні, а сторони пропорційні).
Для гомотетичних фігур і діють формули відношення периметрів і площ подібних фігур.
Зверни увагу!
Будь-які два кола гомотетичні.
Аби гомотетія була визначена, повинен бути заданий центр гомотетії і коефіцієнт.
Це можна записати: гомотетія \((O; k).\)
На малюнку з фігури можна отримати фігуру гомотетією \((O; 2).\)
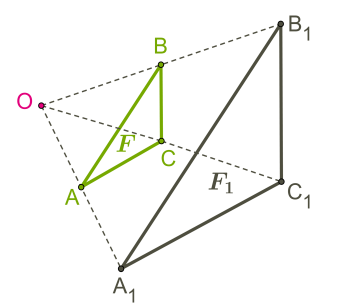
Якщо фігури розташовані на протилежних напрямах від центру гомотетії, то коефіцієнт від'ємний.
На наступному малюнку з фігури можна отримати фігуру гомотетією \((O; - 2).\)
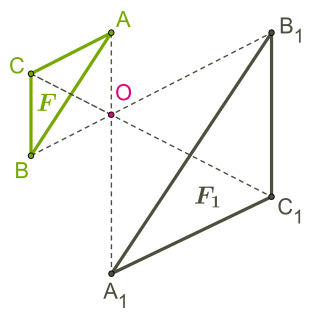
Центр гомотетії може розташовуватися і всередині фігури.
Сірий трикутник із зеленого трикутника \(ABC\) отриманий гомотетією \(.\)
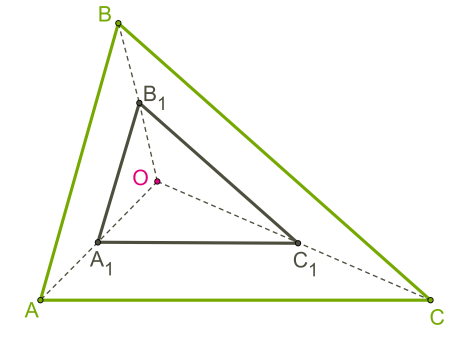
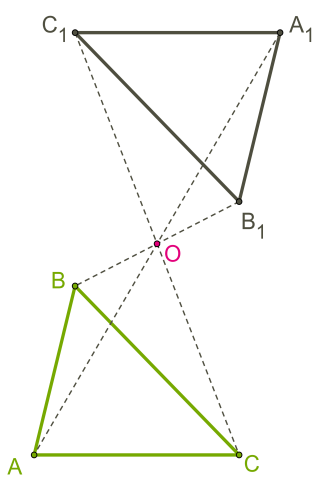
Гомотетія \((O; -1)\) — це центральна симетрія або поворот на \(180°.\)
У даному випадку фігури однакові.
Зверни увагу!
На відміну від гомотетії, геометричні перетворення (центральна симетрія, осьова симетрія, поворот, паралельне перенесення) є рухом, тому в них фігура відображається у фігуру, рівну даній.
Гомотетичні фігури подібні, але подібні фігури не завжди гомотетичні (в гомотетії важливе розташування фігур).
В орнаментах (на малюнку — фрактали) можна бачити безліч подібних фігур, але зазвичай вони не гомотетичні, тому в них неможливо визначити центр гомотетії.

