Рух — це відображення площини на себе, при якому зберігаються відстані між точками.
Якщо дві фігури поєднати одну з одною за допомогою руху, то ці фігури будуть однакові, рівні.
Один із таких рухів — осьова симетрія. Кожній точці на площині за певним законом ставиться у відповідність інша точка тієї самої площини.
Закон такий:
\(1.\) Із точки \(M\) проводиться перпендикуляр до осі симетрії (прямої) і виходить точка \(P\) — точка перетину перпендикуляра з віссю.
\(2.\) На перпендикулярі відкладається відрізок і розташовується точка \(.\)
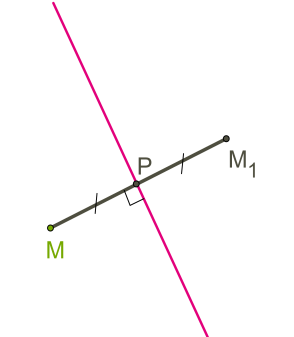
Отже, будь-якій точці \(M\) площини ставиться у відповідність єдина точка площини.
Осьова симетрія є окремим випадком так званого відображення площини на себе.
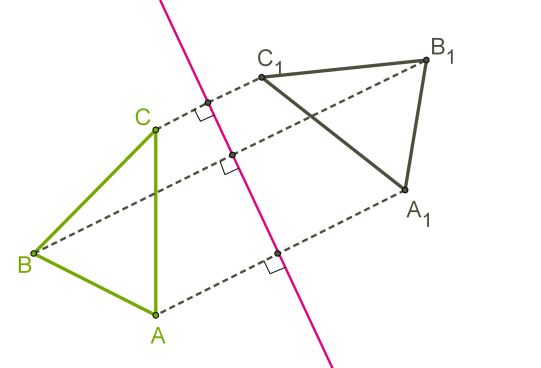
Щоб відобразити фігури в симетрії відносно прямої, достатньо відобразити відповідні вершини.
Іншим окремим випадком відображення площини на себе є центральна симетрія.
Точка площини \(M\) переходить у точку площини за наступним законом:
\(1.\) Із точки \(M\) проводиться пряма, що з'єднує точку з центром симетрії (точкою \(O).\)
\(2.\) На прямій відкладається відрізок і розташовується точка \(.\)
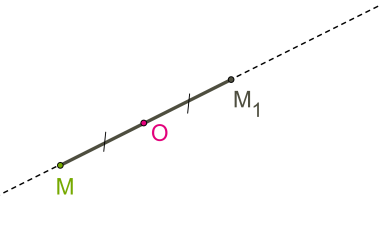
ставиться у відповідність точці \(M.\)
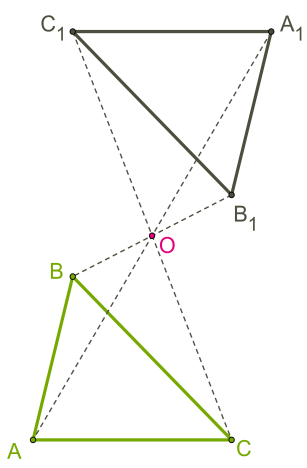
Щоб відобразити фігури в симетрії відносно точки, достатньо відобразити відповідні вершини.
Зверни увагу!
Обидва наведених приклади відображень мають наступні властивості:
\(1.\) Кожен відрізок даної довжини переходить у відрізок тієї самої довжини, тобто відстані між будь-якими точками зберігаються.
\(2.\) Промінь переходить у промінь, пряма — у пряму.
\(3.\) Під час руху фігура відображається в рівну їй фігуру.
\(4.\) Рух є оберненим. Відображення, зворотне руху, є рухом.
\(5.\) Композиція двох рухів також є рухом.
\(1.\) Кожен відрізок даної довжини переходить у відрізок тієї самої довжини, тобто відстані між будь-якими точками зберігаються.
\(2.\) Промінь переходить у промінь, пряма — у пряму.
\(3.\) Під час руху фігура відображається в рівну їй фігуру.
\(4.\) Рух є оберненим. Відображення, зворотне руху, є рухом.
\(5.\) Композиція двох рухів також є рухом.
Іноді в природі спостерігаємо щось схоже на дзеркальну симетрію відносно площини:

