Ламана
Ламаною називається фігура, яка складається з точок і відрізків, що їх з'єднують.
Точки називаються вершинами ламаної, а відрізки — ланками ламаної.
Види ламаних
Ламана називається замкненою, якщо в неї збігаються кінці.
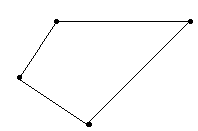
Якщо кінці ламаної не збігаються, вона називається незамкненою.
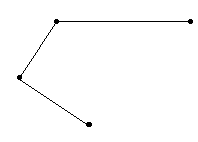
Ламана називається простою, якщо вона не має самоперетинів.
Обидві намальовані вище ламані є простими.
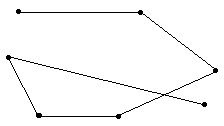
На наступному малюнку зображено ламану з самоперетином.
Многокутник
Многокутник — це проста замкнена ламана лінія і кінцева частина площини, яку вона обмежує.
Вершини ламаної лінії називаються вершинами многокутника, а її ланки — сторонами многокутника.
Відрізки, які з'єднують вершини і не належать одній стороні, називаються діагоналями многокутника.
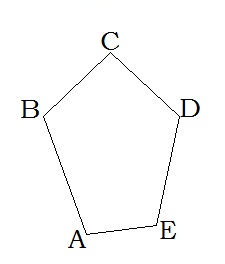
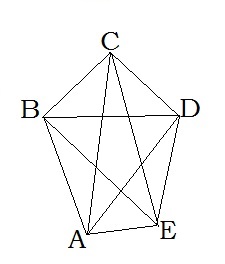
\(A,\) \(B,\) \(C,\) \(D,\) \(E\) — вершини;
\(AB,\) \(BC,\) \(CD,\) \(DE,\) \(AE\) — сторони;
\(AC,\) \(AD,\) \(BE,\) \(BD,\) \(CE\) — діагоналі.
Многокутник, у якого всі кути менші, ніж \(180\)\(,\) називається опуклим многокутником.
П'ятикутник \(ABCDE\) є опуклим многокутником.
Сума кутів опуклого \(n\)-кутника
У загальному випадку многокутник можна назвати \(n\)-кутником. Це означає, що в даного многокутника \(n\) сторін та \(n\) вершин.
Сума кутів опуклого \(n\)-кутника дорівнює \(.\)
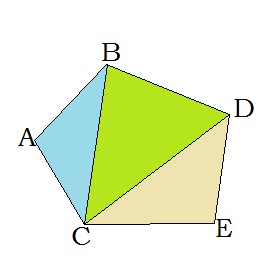
Будь-який опуклий многокутник можна поділити на трикутники. Кількість трикутників на \(2\) менша, ніж кількість сторін у многокутнику.
Сума внутрішніх кутів будь-якого трикутника дорівнює \(180\)\(.\)
Тому сума кутів опуклого \(n\)-кутника дорівнює \(.\)
Приклад:
Обчисли суму внутрішніх кутів опуклого одинадцятикутника.
Можна намалювати малюнок, але це необов'язково для розв'язання завдання.
Використаємо формулу:
