Правильними називаються многокутники, в яких усі сторони та кути рівні.
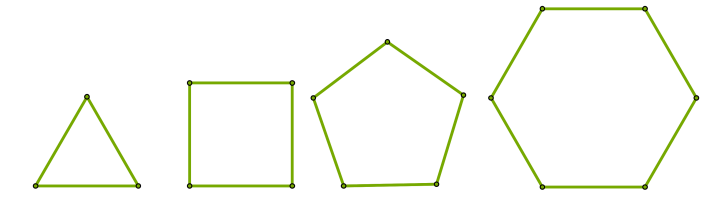
На малюнку бачимо деякі правильні многокутники: трикутник, чотирикутник (квадрат), п'ятикутник і шестикутник.
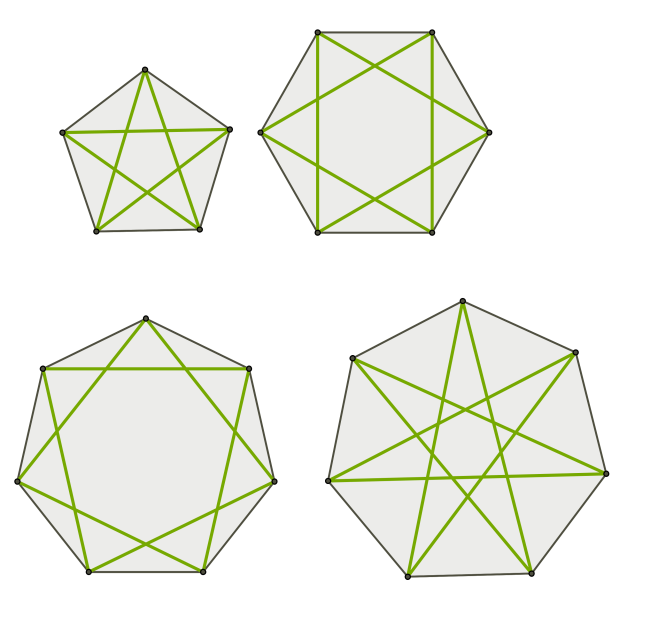
Якщо в правильних опуклих многокутниках провести діагоналі, то утворяться правильні увігнуті многокутники: із діагоналей п'ятикутника отримаємо пентаграму, з діагоналей шестикутника — гексаграму, а з діагоналей семикутника — дві різні гептаграми.
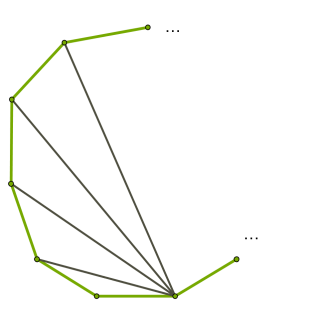
Якщо провести всі діагоналі з однієї вершини, будь-який \(n\)-кутник можна поділити на \(n\) \(-\) \(2\) трикутники.
Отже, сума всіх внутрішніх кутів визначається за формулою \(.\)
Оскільки всі кути правильного \(n\)-кутника рівні, то величина одного внутрішнього кута дорівнює:
Навколо будь-якого правильного многокутника можна описати і вписати в нього коло. При цьому збігаються центри обох кіл, і цю точку називають центром многокутника.
Вписане коло належить усім сторонам, описане коло проходить через усі вершини.
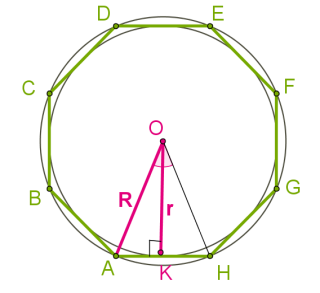
У трикутнику \(AOK\) пов'язані сторона \(a\) (половина сторони \(AK\)), радіус описаного кола \(OA = R\) і радіус вписаного кола \(OK = r.\)
Оскільки \(n\)-кутник складається з \(n\) трикутників, рівних \(AOH,\) то:
Для правильного трикутника і квадрата додатково діють усі формули, які були розглянено в курсі геометрії.
