У системі координат побудуємо півколо з радіусом \(1\) та центром у початку координат.
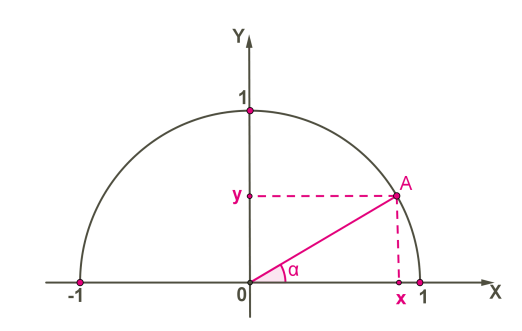
Як уже відомо, в прямокутному трикутнику синус гострого кута визначається як відношення протилежного катета до гіпотенузи, а косинус гострого кута — як відношення прилеглого катета до гіпотенузи.
У трикутнику \(AOX:\)
Оскільки радіус півкола \(R = AO = 1,\) то \(.\)
Довжина відрізка \(AX\) дорівнює величині координати \(y\) точки \(A,\) а довжина відрізка \(OX\) — величині координати \(x\) точки \(A:\)
Отже, для кутів бачимо, що \(.\)
У прямокутному трикутнику тангенс гострого кута дорівнює відношенню протилежного катета до прилеглого катета. Отже:
Використовуючи одиничне півколо та розглянену інформацію, визначимо синус, косинус і тангенс для \(.\)
Розглянемо обидва гострих кути в трикутнику \(AOX.\) Якщо разом вони утворюють \(,\) то обидва виразимо через \(:\)
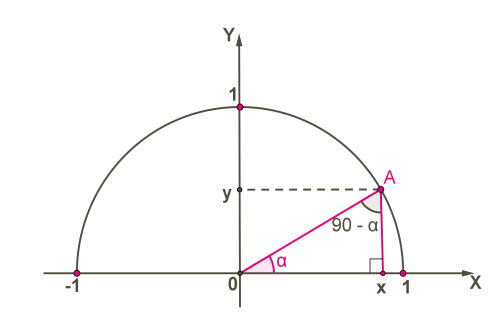
Якщо \(,\) то \(.\)
Ми бачимо, що правильними є рівності:
Розглянемо тупий кут, який також виразимо через \(:\)
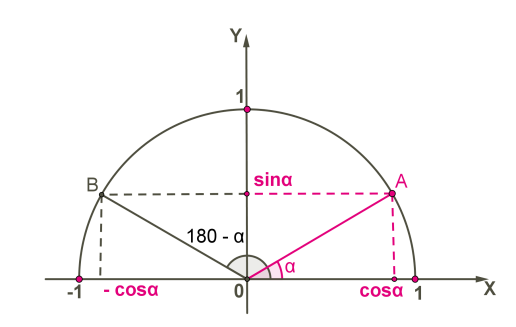

Правильними є наступні рівності:
Ці формули називаються формулами зведення:
Якщо в трикутнику \(AOX\) застосувати теорему Піфагора, отримаємо \(.\) Замінивши відрізки, відповідно, на синус і косинус, запишемо головну тригонометричну тотожність:
Ця тотожність дозволяє обчислити величину синуса кута, якщо відомий косинус
(як уже зазначено, синус для кутів лише \(0\) або додатний):
(як уже зазначено, синус для кутів лише \(0\) або додатний):
або величину косинуса кута, якщо відомий синус:
Для гострих кутів косинус додатний, а для тупих кутів беремо від'ємне значення.
