Теорема синусів
Теорему Піфагора і тригонометричні функції гострого кута можна використовувати для обчислення елементів лише в прямокутному трикутнику.
Для знаходження елементів у довільному трикутнику використовується теорема синусів або теорема косинусів.
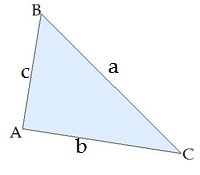
Теорема синусів
Сторони трикутника пропорційні синусам протилежних кутів:
(під час розв'язання задачі одночасно пишуться дві частини, утворюючи пропорцію).
Теорема синусів використовується для обчислення:
\(1)\) невідомих сторін трикутника, якщо відомі два кути і одна сторона;
\(2)\) невідомих кутів трикутника, якщо відомі дві сторони і один прилеглий кут.
Оскільки один із кутів трикутника може бути тупим, значення синуса тупого кута знаходиться за формулою зведення:
.
Найчастіше використовуються тупі кути:
Радіус описаного кола
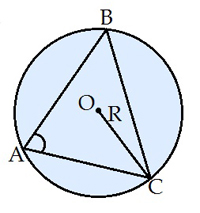
\(,\) де \(R\) — радіус описаного кола.
Виразивши радіус, отримуємо \(,\) або \(,\) або \(.\)
Теорема косинусів
Для обчислення елементів прямокутного трикутника достатньо \(2\) дані величини (дві сторони або сторона і кут).
Для обчислення елементів довільного трикутника необхідно хоча б \(3\) дані величини.

Теорема косинусів
Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін на косинус кута між ними:
Також теорема виконується для будь-якої сторони трикутника:
Теорема косинусів використовується для обчислення:
\(1)\) невідомої сторони трикутника, якщо відомі дві сторони і кут між ними;
\(2)\) обчислення косинуса невідомого кута трикутника, якщо відомі всі сторони трикутника.
Значення косинуса тупого кута знаходиться за формулою зведення:
.
Найчастіше використовуються тупі кути:
Якщо необхідно знайти приблизне значення синуса або косинуса іншого кута або обчислити кут за знайденим синусом чи косинусом, використовується таблиця або калькулятор.
