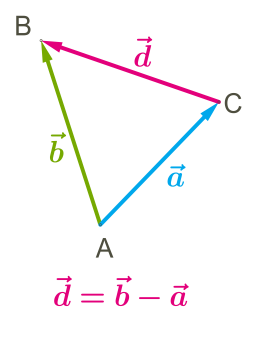
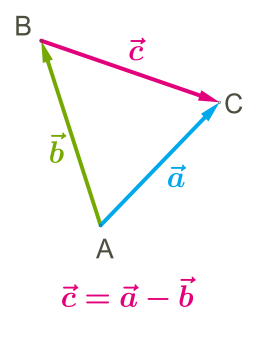
Аби краще зрозуміти закон віднімання векторів, потрібно пригадати властивість математичних дій: додавання і віднімання.
Якщо \(,\) то \(.\)
Така сама властивість правильна і для дій із векторами.
Щоб відняти вектор від вектора \(,\) потрібно знайти такий вектор \(,\) сумою якого з вектором був би вектор \(.\)
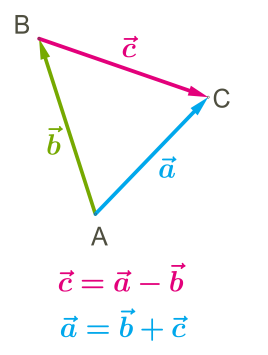
Зверни увагу!
Легше запам'ятати, як знайти різницю векторів і наступним чином:
\(1)\) вектори потрібно звести до спільного початку \(A;\)
\(2)\) з'єднати кінцеві точки \(B\) і \(C;\)
\(3)\) напрям вектора — різниця кінцевої точки другого вектора та кінцевої точки першого вектора.
Пригадаймо закон паралелограма для додавання векторів.
За цим законом, вектор суми двох векторів, що лежать на сторонах паралелограма зі спільною вершиною, проходить по довгій діагоналі паралелограма. Очевидно, що вектор різниці проходить по короткій діагоналі паралелограма.
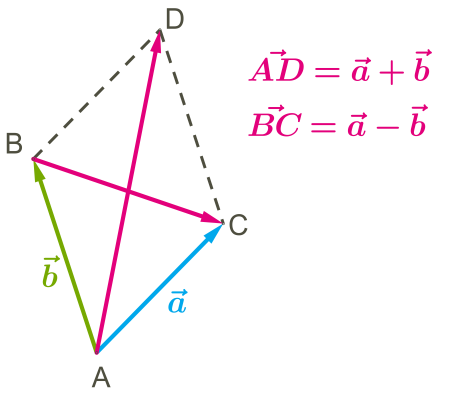
Зауважмо, що при відніманні вектора від вектора вектор різниці буде протилежний вектору \(,\) тобто \(.\)