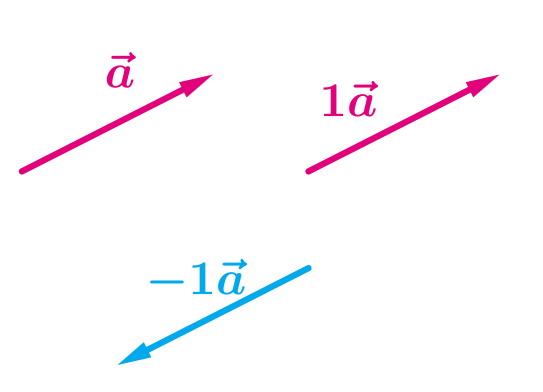Добутком вектора на число \(k\) \((\)\(\)\()\) називається вектор \(\)\(,\) модуль якого дорівнює \(\)\(,\) при цьому:
- вектори і співнапрямлені, якщо \(k > 0;\)
- вектори і протилежно напрямлені, якщо \(k < 0.\)
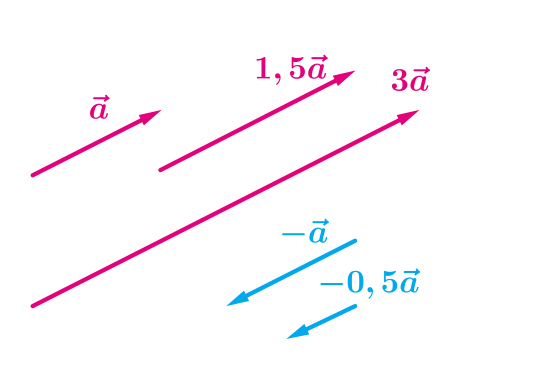
При множенні вектора на число даний вектор і результат колінеарні.
Правильним є таке судження:
Два ненульових вектори і колінеарні тоді й тільки тоді, коли існує таке число \(k,\) при якому виконується рівність \(.\)
Зверни увагу!
Якщо помножити вектор на число \(1,\) отримаємо рівні вектори.
Якщо помножити вектор на число \(-1,\) отримаємо протилежні вектори.