Поняття вектора
Накреслимо якийсь відрізок \(AB.\) Один кінець \(A\) назвемо початковою точкою, а другий \(B\) — кінцевою точкою.
Напрям відрізка \(AB\) з точки \(A\) в точку \(B\) позначимо за допомогою стрілки. Отримаємо спрямований відрізок (див. іл. нижче).
Спрямований відрізок називається вектором.
Вектор можна позначити:
- двома великими буквами, поставивши над ними стрілочку; перша буква позначає початкову точку, друга — кінцеву точку; наприклад, (читається: вектор \(AB\));
- маленькою буквою зі стрілочкою над нею, наприклад, (читається: вектор \(a\)).
Якщо початкова та кінцева точки вектора збігаються, виходить нульовий вектор, який позначається як \(.\)
Будь-яку точку на площині можна вважати нульовим вектором.
Довжина відрізка \(AB\) називається довжиною, або модулем вектора і позначається як \(.\)
Довжина нульового вектора дорівнює нулю:
Величини
Величини, з якими зустрічаємося в природничих науках, бувають скалярними або векторними.
Скалярними називаються величини, що мають числове значення, але не мають напряму.
Векторними величинами, або векторами, називаються величини, що мають і числове значення, і напрям.
Наприклад, якщо сказано, що автомобіль рухається зі швидкістю \(100\) \(км / год\) (тобто дано числове значення швидкості), то про його швидкість відомо не все, адже невідомо, куди і в якому напрямі він рухається.
Приклади векторних величин: швидкість, сила, переміщення.
Зверни увагу!
Переміщенням рухомої точки в даний момент часу називають вектор із початком у точці початку її руху, і кінцем у точці її розташування в даний момент.
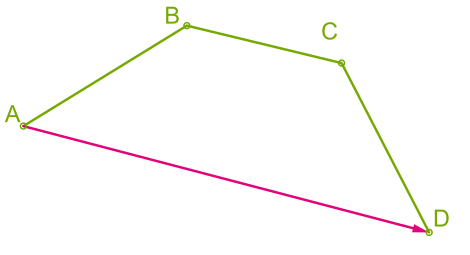
Запам'ятай відмінність між відстанню і переміщенням
Відстань характеризується лише числовим значенням, наприклад, \(AB + BC + CD = 5\) \(км.\)
Відстань — скалярна величина.
Переміщення — вектор \(,\) що сполучає початкове й кінцеве положення тіла, і його довжина не дорівнює \(5\) \(км.\)
Переміщення — векторна величина.
Наприклад, можна проїхати \(5\) \(км\) і повернутися назад. Переміщення ж у цьому випадку дорівнюватиме \(0\) і позначатиметься як нульовий вектор.
