Скалярний добуток векторів — урок. Геометрія, 9 клас.

Скалярним добутком двох векторів

\vec{a}

і

\vec{b}

буде скалярна величина (число), що дорівнює добутку модулів цих векторів, помножене на косинус кута між ними:

\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos α

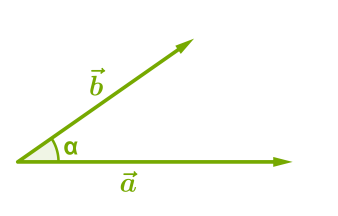
Дуже важливо правильно визначати кут між векторами. Якщо вектори не мають спільної початкової точки, необхідно уявити, який кут утворився б, якби їх перемістили до спільної початкової точки.

Кут між векторами позначають

\hat{\vec{a} \vec{b}} = α

\(.\)

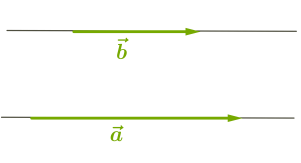
\(1.\) Якщо вектори співнапрямлені, то

\hat{\vec{a} \vec{b}} = 0 °

\(:\)

Зверни увагу!

Оскільки косинус кута величиною \(0°\) дорівнює \(1,\) то скалярний добуток співнапрямлених векторів є добутком їхніх довжин.

Якщо два вектори рівні, то такий скалярний добуток називають скалярним квадратом.

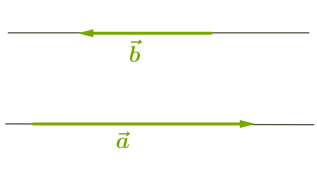
\(2.\) Якщо вектори протилежно напрямлені, то

\hat{\vec{a} \vec{b}} = 180 °

\(:\)

Зверни увагу!

Оскільки косинус кута величиною \(180°\) дорівнює \(-1,\) то скалярний добуток протилежно напрямлених векторів дорівнює від'ємному добутку їхніх довжин.

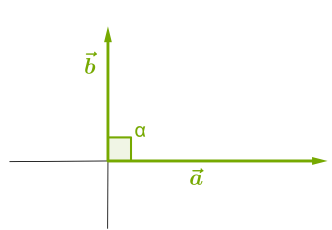
\(3.\) Вектори називають перпендикулярними, якщо

\hat{\vec{a} \vec{b}} = 90 °

\(:\)

Зверни увагу!

Оскільки косинус прямого кута дорівнює \(0,\) то скалярний добуток перпендикулярних векторів дорівнює \(0.\)

\(4.\) Потрібно уважно розглянути випадки, коли вектори утворюють тупий кут:

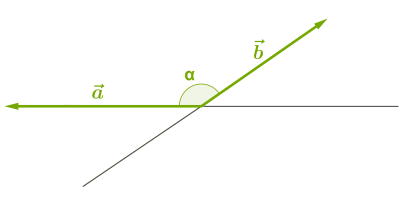
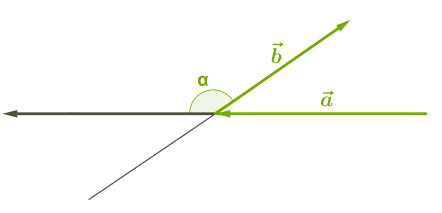
Зверни увагу!

Оскільки косинус тупого кута від'ємний, то скалярний добуток векторів, які утворюють тупий кут, є від'ємним.

Скалярний добуток векторів, заданих координатами

Якщо

\vec{a} (x_{a}; y_{a})

і

\vec{b} (x_{b}; y_{b})

\(,\) то

\vec{a} \cdot \vec{b} = x_{a} \cdot x_{b} + y_{a} \cdot y_{b}

\(.\)

Оскільки в координатах

|\vec{a}| = \sqrt{{x_{a}}^{2} + {y_{a}}^{2}}

і

|\vec{b}| = \sqrt{{x_{b}}^{2} + {y_{b}}^{2}}

\(,\) то можна визначити косинус кута між векторами, а отже й величину кута.

\begin{array}{l} \cos α = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|} \\ \cos α = \frac{x_{a} \cdot x_{b} + y_{a} \cdot y_{b}}{\sqrt{{x_{a}}^{2} + {y_{a}}^{2}} \cdot \sqrt{{x_{b}}^{2} + {y_{b}}^{2}}} \end{array}

Властивості скалярного добутку векторів

\(1.\) Скалярний добуток вектора самого на себе завжди більший або дорівнює нулю.

Скалярний добуток вектора самого на себе дорівнює нулю тоді й тільки тоді, коли вектор дорівнює нульовому вектору:

\vec{a} \cdot \vec{a} > 0; \vec{0} \cdot \vec{0} = 0

\(2.\) Скалярний добуток вектора самого на себе дорівнює квадрату його модуля:

\vec{a} \cdot \vec{a} = {|\vec{a}|}^{2}

\(3.\) Для скалярного добутку діє переставний закон:

\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}

\(4.\) Для скалярного добутку діє розподільний закон:

(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}

\(5.\) Для скалярного добутку діє сполучний закон:

(k \cdot \vec{a}) \cdot \vec{b} = k \cdot (\vec{a} \cdot \vec{b})

\(6.\) Якщо скалярний добуток двох ненульових векторів дорівнює нулю, то ці вектори перпендикулярні.

Попередня тема

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!