Рівняння кола
Використаємо два відомих факти і виведемо рівняння кола:
\(1.\) Усі точки кола розташовані на даній відстані (радіус) від даної точки (центр).
\(2.\) Ми маємо формулу для розрахунку відстані між двома точками, якщо знаємо координати точок \(,\) а якщо так, то квадрат відстані:
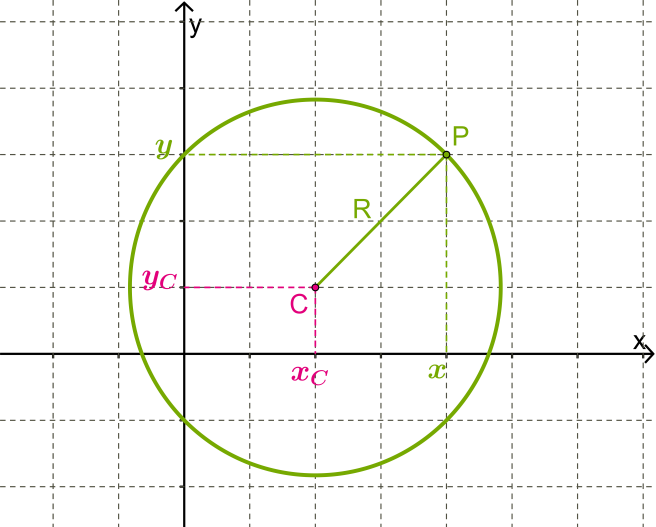
Припустимо, що центр кола розташовується в точці \(,\) а радіус кола дорівнює \(R.\)
Будь-яка точка на цьому колі розташована на відстані \(R\) від центру \(C,\) отже правильною є рівність:
Це і є рівняння кола з центром \(C\) і радіусом \(R.\) Координати всіх точок, які розташовані на колі, задовольняють рівняння.
Якщо центр кола розташований на початку координат \(,\) то рівняння має наступний вигляд:
Загальне рівняння прямої
Відомо, що всі точки серединного перпендикуляра розташовані на рівних відстанях від кінців відрізка.
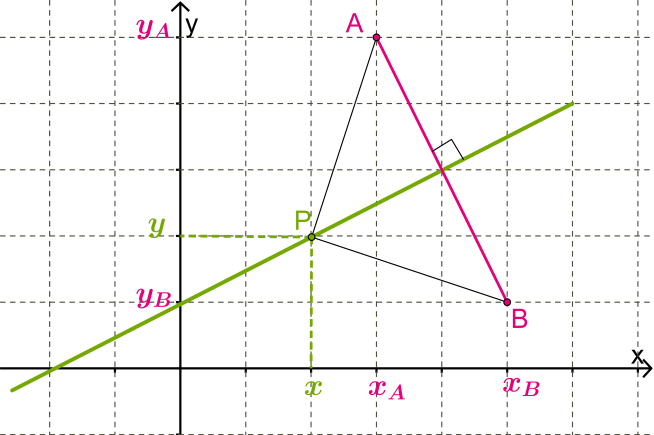
Координати кінців відрізка: і
Будь-яка точка розташовується на рівних відстанях від кінцевих точок \(.\)
Звісно, рівні й квадрати відстаней \(,\) тож правильною є рівність
\(,\) яка і є рівнянням прямої.
Після зведення виразів у дужках і зведення подібних доданків:
рівняння матиме такий вигляд:
Рівняння прямої у прямокутній системі координат має вигляд , де \(a\), \(b\), \(c\) — числа, причому \(a\) і \(b\) одночано не дорівнюють нулю.
Рівняння ще називають загальним рівнянням прямої.
Рівняння прямої, що проходить через дві задані точки
Складемо рівняння прямої, що проходить через точки і та складається за пропорцією різниць відповідних координат.
Воно має вигляд:
, якщо .
Дану формулу ще називають канонічним рівнянням прямої.
Розглянемо на прикладі, як скласти рівняння прямої, що проходить через точки \(A(3;4)\) та \(B(8;10)\).
Розвязання: Використовуючи канонічне рівняння, маємо:
звідки .
З отриманого рівняння прямої, можна визначити запис рівняння прямої з кутовим коефіціентом:
.
Особливі прямі
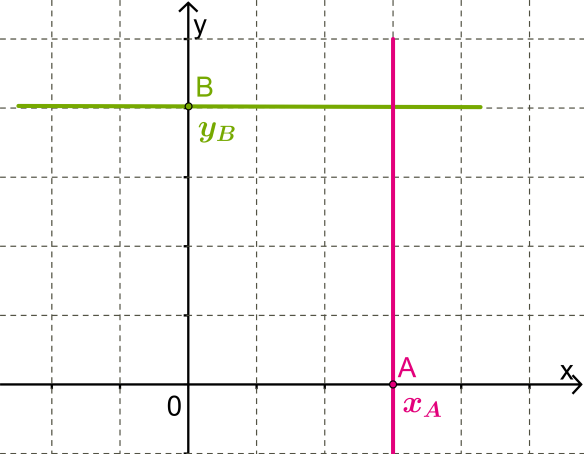
\(1.\) Пряма проходить через деяку точку на осі \(Ox\) з координатами \(.\)
Для будь-якої точки на цій прямій \(.\) Це і є рівняння прямої.
Оскільки вісь \(Oy\) проходить через початок координат, то рівнянням осі \(Oy\) є \(.\)
\(2.\) Пряма проходить через деяку точку на осі \(Oy\) з координатами \(.\)
Для будь-якої точки на цій прямій \(,\) це і є рівняння прямої.
Оскільки вісь \(Ox\) проходить через початок координат, то рівнянням осі \(Ox\) є \(.\)
