Якщо вектор розташувати на осі координат так, що його початок знаходитиметься на початку координат, то координати цього вектора дорівнюватимуть координатам його кінцевої точки \(.\)
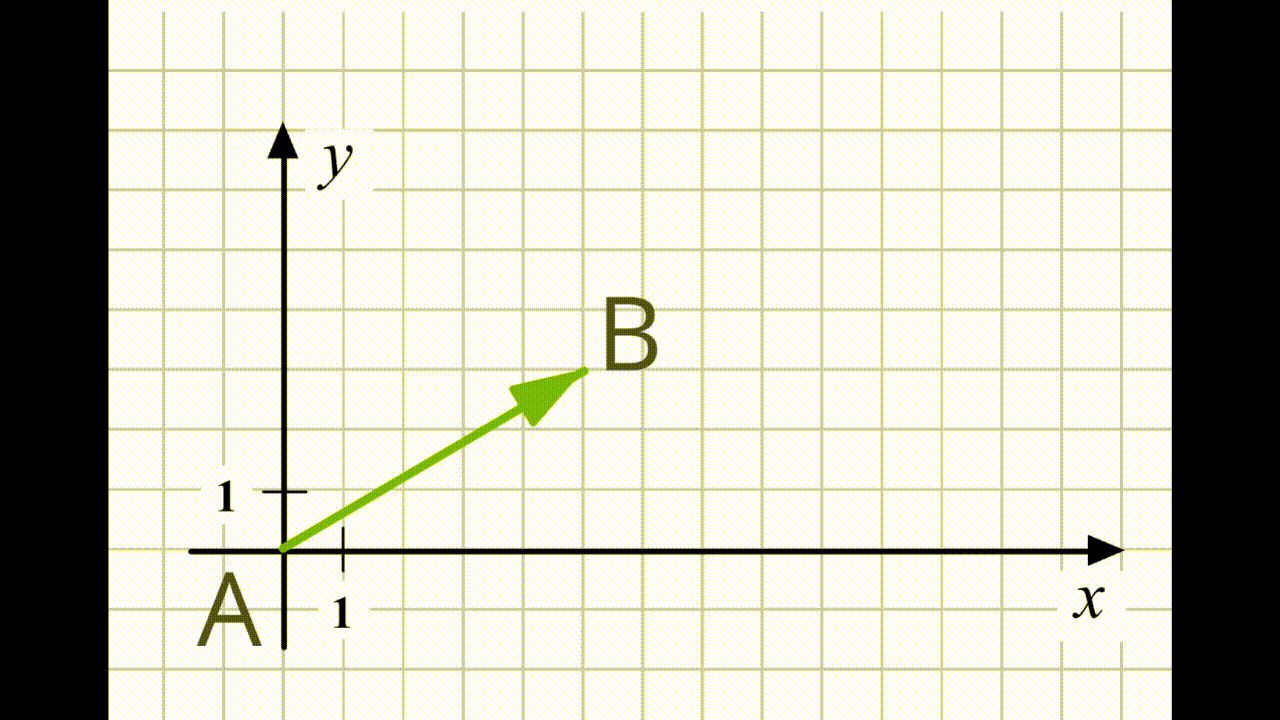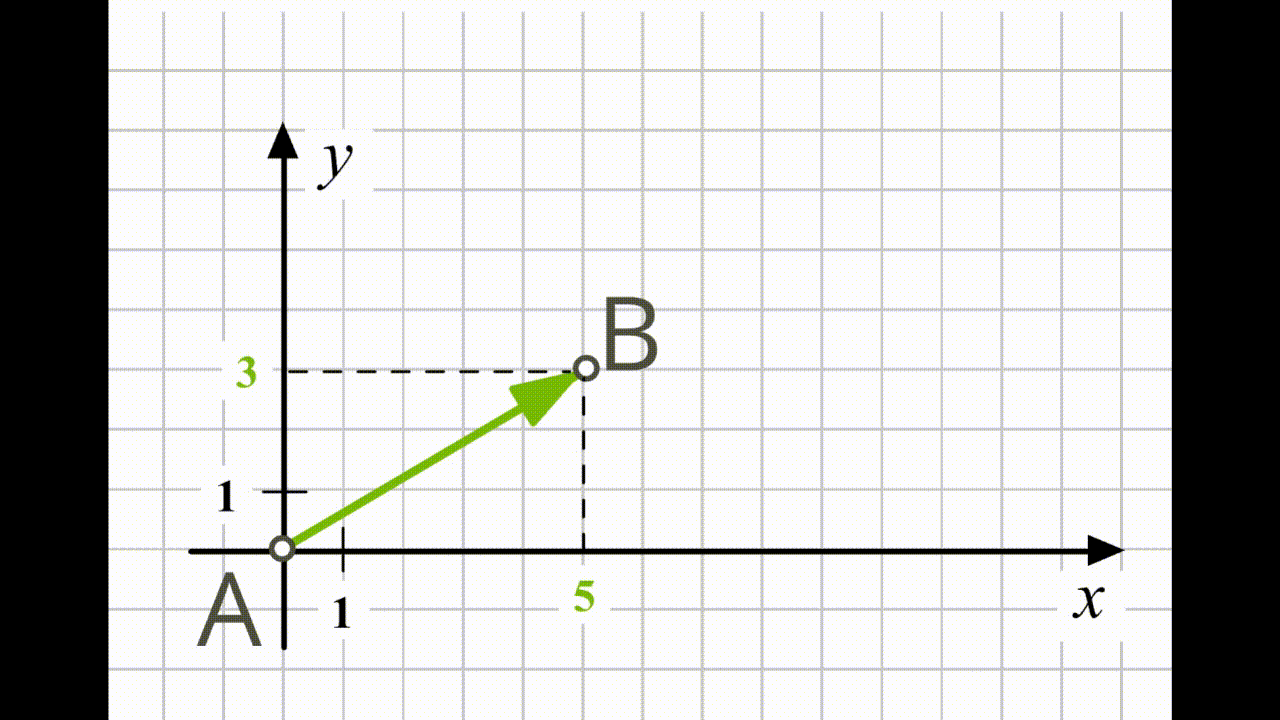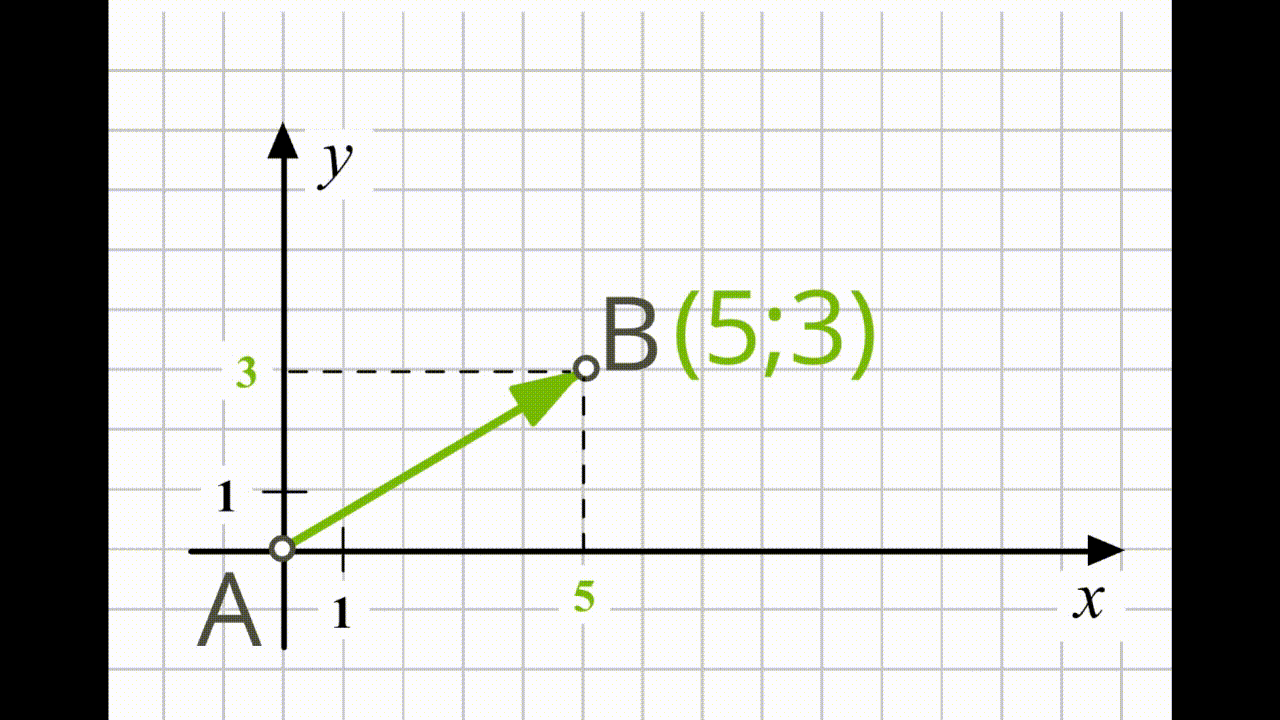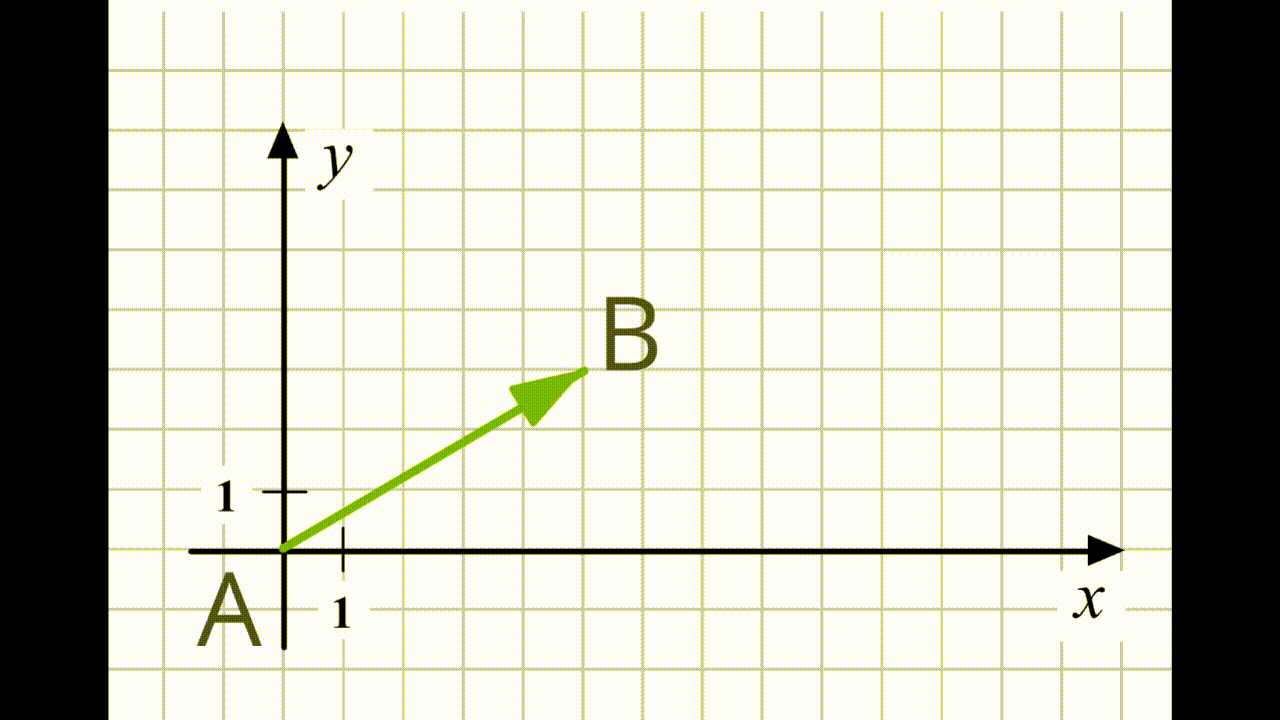
Координати вектора, поданого на малюнку, дорівнюють \(.\) У цьому випадку координати вектора збігаються з координатами його кінця \(B.\)
Координатами вектора є координати кінцевої точки цього вектора, якщо вектор розташований так, що його початок знаходиться на початку координат.
Якщо і \(,\) то координати вектора дорівнюють \(.\)

Приклад:
Маємо точки \(A (-2; 2)\) і \(B (3; 5).\) Потрібно визначити координати вектора \(.\)
Розв'язання:
\(= (3 - (-2) ; 5 - 2) = (5; 3)\)
Отримано вектор із такими ж координатами, як на першому малюнку.
Перенісши початок даного вектора в початок координат \((0; 0),\) отримуємо такий же вектор (із тим же напрямом і довжиною).
Дії з векторами в координатній формі
Якщо дано вектори і \(,\) то: