У програмах можна поєднувати команди розгалуження та повторення. Ми вже складали алгоритми, у яких команди розгалуження та повторення слідували одна за одною.
Але команди можуть також міститися одна в одній: розгалуження можуть бути вкладені як у цикл із параметром, так і в цикл із передумовою.
Розгалуження, вкладене в цикл із параметром
Цикл for перебирає елементи деякої послідовності значень. Якщо при цьому потрібно перевірити, чи відповідає кожний елемент послідовності певній умові, в тіло циклу слід вкласти команду розгалуження. Розгалуження, вкладене в цикл, може бути повним і неповним. Приклад:
На квітнику 7 квіток. Підрахуємо кількість червоних і кількість синіх квіток. Блок-схема команди циклу, яка виконує такий підрахунок, наведена на рис.1.
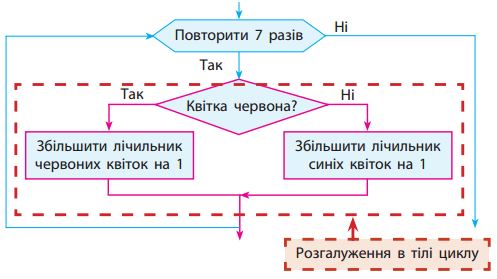
Рис.1
Приклад:
Знайдемо кількість слів red у заданій послідовності.
kred = kblue = 0 # Задання початкових значень лічильника
for word in ['blue', 'red', 'red', 'blue', 'red', 'blue', 'red']: # Послідовність задана списком
if word == 'red': # Якщо змінна циклу набуває значення 'red'
kred = kred+1
else: kblue = kblue+1 # Якщо word == 'blue'
print('kred = ', kred, 'kblue = ', kblue)
kred = kblue = 0 # Задання початкових значень лічильника
for word in ['blue', 'red', 'red', 'blue', 'red', 'blue', 'red']: # Послідовність задана списком
if word == 'red': # Якщо змінна циклу набуває значення 'red'
kred = kred+1
else: kblue = kblue+1 # Якщо word == 'blue'
print('kred = ', kred, 'kblue = ', kblue)
Приклад:
Введемо з клавіатури 8 довільних чисел і серед введених чисел підрахуємо кількість парних (рис. 2).
k = 0 # Задання початкового значення лічильника
for i in range(8): # Повторити команди тіла циклу для всіх чисел від 0 до 7
a = int(input('Наступне число'))
if a%2 == 0: # Вкладене неповне розгалуження перевіряє,
k = k+1 # чи дорівнює нулю остача від ділення
print('Кількість парних дорівнює ', k) # числа а на 2
k = 0 # Задання початкового значення лічильника
for i in range(8): # Повторити команди тіла циклу для всіх чисел від 0 до 7
a = int(input('Наступне число'))
if a%2 == 0: # Вкладене неповне розгалуження перевіряє,
k = k+1 # чи дорівнює нулю остача від ділення
print('Кількість парних дорівнює ', k) # числа а на 2

Рис.2
Приклад:
Серед восьми додатних чисел, які вводяться з клавіатури, визначимо найбільше.
m = –1 # Задавання початкового значення змінної,
for i in range(8): # у якій зберігатиметься найбільше значення
a = int(input('Наступне число')) # Уведення і-го числа
if a>m: m = a # Якщо введене число більше поточного
# значення m, замінити m уведеним числом
print('Найбільше число ', m)
m = –1 # Задавання початкового значення змінної,
for i in range(8): # у якій зберігатиметься найбільше значення
a = int(input('Наступне число')) # Уведення і-го числа
if a>m: m = a # Якщо введене число більше поточного
# значення m, замінити m уведеним числом
print('Найбільше число ', m)
Приклад:
Знайдемо всі дільники натурального числа k. Число 1 і саме число k не включаємо до переліку дільників.
Алгоритм розв’язування задачі: перебрати всі значення числа і від 2 до k//2; якщо і є дільником числа k (k%і == 0), вивести значення і.
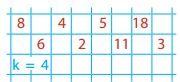
Результат виконання наведено на рис. 3.
k = int(input('k = ?'))
for i in range(2, k//2+1):
if k%i == 0: print(i, ' ', end = '')
Алгоритм розв’язування задачі: перебрати всі значення числа і від 2 до k//2; якщо і є дільником числа k (k%і == 0), вивести значення і.
Результат виконання наведено на рис. 3.
k = int(input('k = ?'))
for i in range(2, k//2+1):
if k%i == 0: print(i, ' ', end = '')
Рис.3
Розгалуження, вкладене в цикл із передумовою
У циклах із умовою також можна керувати виконанням команд тіла циклу за допомогою вкладених розгалужень.Алгоритм знаходження НСД(a, b) — найбільшого спільного дільника двох чисел a і b — називають алгоритмом Евкліда, давньогрецького математика. Маємо: поки А ≠ В, від більшого числа віднімати менше (рис. 4).
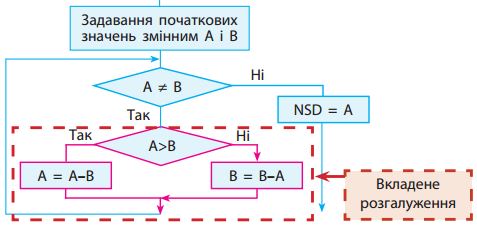
Під час кожної ітерації циклу більше з чисел А і В заміняється їх різницею.
Цикл припиняється, коли значення змінних А і В стають рівними — це НСД початкових значень.
a = int(input('a = ?'))
b = int(input('b = ?'))
while a!=b:
if a>b: a=a-b
else: b=b-a
print ('nsd=', a)
Виконаємо алгоритм для чисел 12 і 18 (рис. 5).
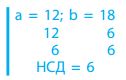
Рис.5
Джерела:
Інформатика : підруч. для 6 кл. закл. загал. серед. освіти / [О. О. Бондаренко, В. В. Ластовецький, О. П. Пилипчук, Є. А. Шестопалов]. — Харків : Вид-во «Ранок», 2023.
