Якщо побудову деякої геометричної фігури оформити як процедуру, то одну цю процедуру можна використовувати для малювання цієїфігури різних розмірів у різних місцях вікна.
Розробимо проєкт з використанням процедури малювання рівнобедреного трикутника з висотою 100. У цієї процедури будуть три аргументи цілого типу: дві координати лівої вершини основи трикутника і довжина основи (рис.1).
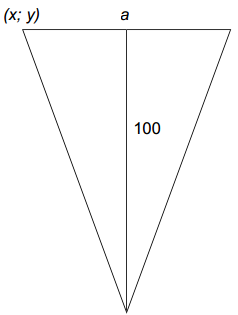
Рис.1
Конкретні значення координат лівої вершини основи трикутника (х; у) передаватимуться процедурі в команді її виклику. Координати правої вершини основи дорівнюватимуть (х+а; у).
Абсциса вершини рівнобедреного трикутника повинна дорівнювати х+а:2, а ордината — у+100. Оскільки координати всіх точок вікна (полотна) повинні бути цілими числами, то для визначення половини довжини основи потрібно використати операцію цілочисельного ділення (//).
На рис.2 наведено текст проєкту малювання трикутників з використанням процедури.
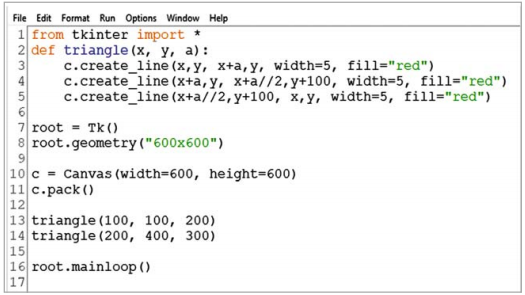
Рис.2
У наведеному тексті проєкту:
у процедурі triangle для малювання трикутника:
- команда c.create_line(x,y, x+a,y, width=5, fill=“red”) малює основу трикутника завдовжки а з точки (х,у) до точки (х+а, у);
- команди c.create_line(x+a,y, x+a//2,y+100, width=5, fill=“red”) і c.create_line(x+a//2,y+100, x,y, width=5, fill=“red”) малюють бічні сторони трикутника;
в основній частині проєкту:
- дві команди виклику процедури triangle:
triangle(100, 100, 200) ; triangle(200, 400, 300);
- аргументами при виклику є конкретні значення двох координат лівої вершини основи трикутника і довжина цієї основи;
- у процесі виконання першої з цих команд змінні х, у, а (аргументи процедури triangle) набувають значень х = 100, у = 100, а = 200, і відбувається виконання
команд процедури triangle з цими значеннями аргументів; в результаті на екрані з'являється рівнобедрений трикутник із заданими координатами лівої вершини основи та довжиною основи; - друга команда виклику виконується аналогічно (рис. 3).
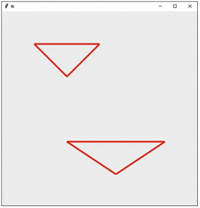
Рис.3
Джерела:
Інформатика : підруч. для 7-го кл. закл. заг. серед. освіти / Йосиф Ривкінд [та ін.]. — Київ : Генеза, 2024.