Розв’язування прикладної задачі на комп'ютері проходить через такі етапи:
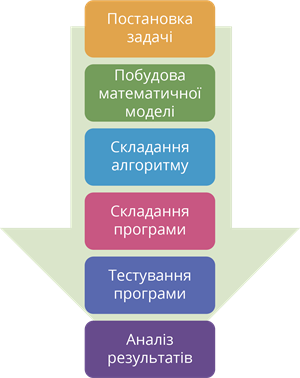
І етап. Постановка задачі.
Розв’язування практичної задачі починається з опису вихідних даних і цілей задачі.
На цьому етапі потрібно чітко визначити умови задачі:
- Що дано?
- Які дані допустимі?
- Які результати, в якому вигляді повинні бути отримані?
ІІ етап. Побудова математичної моделі.
На цьому етапі потрібно розгорнутий змістовний опис задачі замінити її математичною моделлю за допомогою математичних залежностей.
Математична модель — це математичний опис найбільш істотних властивостей реального об'єкта. Для побудови математичної моделі потрібно:
- зрозуміти, в якій предметній галузі шукати опис об’єктів, що є в умові задачі;
- відібрати ознаки, суттєві для задачі, яка розв’язується;
- встановити між необхідними в задачі результатами і вхідними даними зв'язок, який забезпечує розв’язок поставленої задачі.
Математична модель — це система математичних співвідношень між величинами, необхідними для розв’язування задачі.
Математичну модель зручно подавати в такій формі:
Дано: <Перелік початкових даних >
Потрібно: <Перелік потрібних результатів >
Зв’язок: <Система рівнянь або тверджень, що зв’язують вхідні та шукані дані>
При <Умови допустимості початкових даних >
Дано: <Перелік початкових даних >
Потрібно: <Перелік потрібних результатів >
Зв’язок: <Система рівнянь або тверджень, що зв’язують вхідні та шукані дані>
При <Умови допустимості початкових даних >
ІІІ етап. Складання алгоритму. На цьому етапі потрібно скласти алгоритм розв’язування задачі. Властивості алгоритмів вам відомі з 5 класу.
ІV етап. Складання програми за розробленим алгоритмом. Програмування (складання програми) – кодування складеного алгоритму однією з мов програмування.
V етап. Тестування і налагодження програми. На даному етапі проводиться перевірка правильності роботи програми за допомогою тестів і виправлення виявлених помилок.
Тест — це набір спеціально підібраних вихідних даних і результатів, очікуваних при цих даних.
Тестування полягає у порівнянні результатів тестового прикладу з результатами, які отримані після виконання програми. Найчастіше розбіжність результатів роботи програми з тестовими спричиняють недоліки математичної моделі та помилки в алгоритмі. Після тестування доводиться уточнювати та корегувати модель і перевіряти алгоритм.
VІ етап. Аналіз результатів. На завершальному етапі програма виконується з даними, що задані для розв’язування задачі. У випадку невірогідності результатів можлива зміна самого підходу до розв’язання задачі і повернення до етапу побудови математичної моделі для її корегування та уточнення.
Ілюмінатор корабля має форму кола. Вважаємо, що скриня має форму паралелепіпеда. Скриню можна витягти, якщо діаметр ілюмінатора більший хоча б за одну з трьох діагоналей поверхні скрині.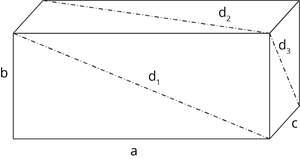 
Нехай R — радіус ілюмінатора, a, b, c — розміри скрині, d1, d2, d3 — діагоналі бічних поверхонь скрині.
Скриню можна просувати через ілюмінатор однією з трьох бічних граней, отже, достатньо, щоб діаметр ілюмінатора виявився більшим хоча б від однієї з трьох діагоналей граней скрині. Для розв’язування задачі необхідно перевірити три умови. Введемо допоміжні змінні Р1, Р2, Р3, які набувають значень 1 або 0 в залежності від виконання відповідної умови.
Дано: R — радіус ілюмінатора,
a, b, c — розміри скрині.
Потрібно: висновок — чи пройде скриня через ілюмінатор.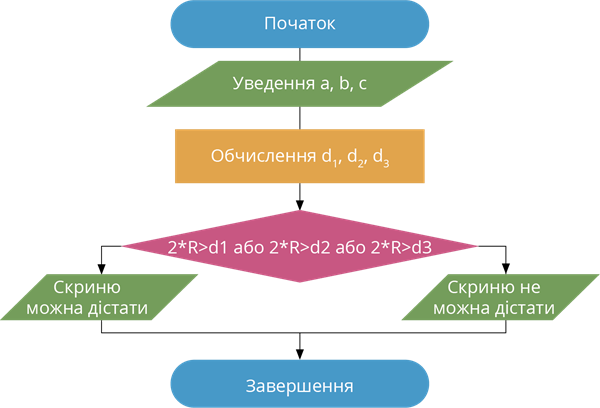 
Приклад:
Через круглий ілюмінатор корабля, що затонув, потрібно витягти скриню з коштовностями. Чи вдасться це зробити?
Ілюмінатор корабля має форму кола. Вважаємо, що скриня має форму паралелепіпеда. Скриню можна витягти, якщо діаметр ілюмінатора більший хоча б за одну з трьох діагоналей поверхні скрині.
Нехай R — радіус ілюмінатора, a, b, c — розміри скрині, d1, d2, d3 — діагоналі бічних поверхонь скрині.
Скриню можна просувати через ілюмінатор однією з трьох бічних граней, отже, достатньо, щоб діаметр ілюмінатора виявився більшим хоча б від однієї з трьох діагоналей граней скрині. Для розв’язування задачі необхідно перевірити три умови. Введемо допоміжні змінні Р1, Р2, Р3, які набувають значень 1 або 0 в залежності від виконання відповідної умови.
Дано: R — радіус ілюмінатора,
a, b, c — розміри скрині.
Потрібно: висновок — чи пройде скриня через ілюмінатор.
Зв’язок: d1 =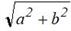 
, d2 = 
, d3 = 
.
, d2 = 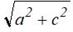, d3 = 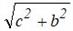. Якщо 2*R> d1 або 2*R> d2 або 2*R> d3, то робимо висновок:
коштовності недоступні, у іншому випадку — скриню можна дістати.
При R>0; a>0; b>0; c>0.
При R>0; a>0; b>0; c>0.
У залежності від зміни умови задачі модель може ускладнюватися і доповнюватися. Наприклад, може знадобитися врахувати вагу скрині — чи зможе водолаз підняти її. Якщо передбачається застосування підйомного механізму, треба враховувати товщину тросів, якими обв’яжуть скриню тощо.
Складемо блок-схему алгоритму:
Реалізуємо алгоритм мовою Python:
import math
import math
a = float(input('a = ?'))
b = float(input('b = ?'))
с = float(input('с = ?'))
b = float(input('b = ?'))
с = float(input('с = ?'))
R = float(input('R = ?'))
d1=math.sqrt (a*a+b*b)
d1=math.sqrt (a*a+b*b)
d2=math.sqrt (a*a+c*c)
d3=math.sqrt (b*b+c*c)
if 2*R>d1 or 2*R>d2 or 2*R>d3:
print ('Скриню можна дістати ')
else:
print ('Скриню не можна дістати ')
Випробуємо програму для різних значень змінних а, b:
а) a=0.8; b=0.5; с=0.5; R=0.4. Відповідь: Скриню можна дістати.
а) a=0.8; b=0.5; с=0.5; R=0.4. Відповідь: Скриню можна дістати.
б) a=1.0: b=0.5; с=0.6; R=0.25. Відповідь: Скриню не можна дістати.