1. Етапи математичного моделювання.

Математичне моделювання застосовується у випадку, коли властивості об’єкта чи явища підлягають описанню математичними формулами.

Проаналізуємо кроки, які потрібно виконати для створення та реалізації математичної моделі задачі:

 

Задача. Улітку учні й учениці 7 класу здійснили подорож на теплоході Дніпром. Шлях униз Дніпром тривав \(a\) годин, а повернення — \(b\) годин. Діти дізналися, що середня швидкість течії Дніпра на цій ділянці становить \(v\) км/год і зацікавилися, з якою швидкістю рухався теплохід. Для пошуку відповіді діти вирішили скласти комп’ютерну програму. 

На цьому етапі потрібно з’ясувати, до якої предметної галузі належать об’єкти, згадані в умові задачі; визначити властивості об’єктів, що є суттєвими для розв’язання задачі; позначити змінні для зберігання значень величин:

Умову задачі тоді можна сформулювати в такий спосіб.
Теплохід пройшов \(a\) годин за течією і \(b\) годин — проти течії. Знайти швидкість руху теплохода в стоячій воді, якщо швидкість течії становить \(v\) км/год (рис.1).

Рис.1 Математичні моделі використовуються

 

2. Побудова математичної моделі
На цьому етапі потрібно розгорнутий опис задачі замінити математичною моделлю за допомогою математичних залежностей.
Для побудови такої моделі слід установити зв’язок між потрібними результатами і вхідними даними (записати рівняння, нерівності), який забезпечує розв’язання завдання.
Запишімо математичну модель задачі.
Що дано? \(a\) — час руху за течією (год); 
                  \(b\) — час руху проти течії (год);
                  \(v\) — швидкість течії (км/год)
Що треба знайти? \(x\) — власна швидкість теплохода (км/год)
Який зв’язок між величинами? \(x = v ·(b + a)/(b – a)\)
Які є обмеження на дані? $0\le a\le b$

3. Реалізація моделі в програмному середовищі
На цьому етапі потрібно розробити алгоритм реалізації моделі; скласти програму за розробленим алгоритмом; виконати тестування і налагодження програми. 

Розробка і складання алгоритму — найважливіший етап розв’язування задачі. Від якості алгоритму залежать правильність результатів, ефективність використання часу й оперативної пам’яті комп’ютера. Алгоритм розв’язування задачі є лінійним (рис.2).

Програмування (складання програми) — кодування складеного алгоритму однією з мов програмування. Ми реалізуємо алгоритм мовою Python:

a = float(input('a = ?'))

b = float(input('b = ?'))
v = float(input('v = ?'))
x = v*(b+a)/(b–a)
print('x = ', x)

 

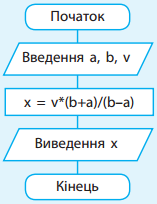
Рис.2

 

На цьому етапі програму потрібно перевірити за допомогою тестів і виправити виявлені помилки.

Найчастіше розбіжність результатів роботи програми з тестовими спричиняють недоліки математичної моделі та помилки в алгоритмі.

Випробуємо програму на такому тесті: при \(а=4,0, b=4,48, v=1,5\) результатом має бути значення \(x = 26,5\).

Отримаємо результат: \(x=26,49999999999998≈26,5\), який збігається з наведеним у тесті.

4. Дослідження створеної комп’ютерної моделі
На цьому етапі можна провести комп’ютерний експеримент, який відповідає цілям моделювання. Він має супроводжуватися осмисленням підсумків, аналізуванням результатів моделювання, що є основою для прийняття рішень.

Слід запустити програму з даними умови задачі і здійснити аналіз отриманих результатів. Змінюючи вхідні дані, можна аналізувати взаємозв’язок між значеннями властивостей об’єкта.