1. Методи сортування масивів

 

Під час опрацювання таблиць часто виникає потреба впорядкувати дані в таблиці за деякою ознакою. Числові дані можна відсортувати за величиною (наприклад, розташування в масиві значень маси деталей за зростанням), рядкові дані — в алфавітному порядку (упорядкування списку учнів).
Клас List у Python має метод sort(): 

де reverse — необов'язковий параметр, що вказує тип сортування.

 

За замовчуванням сортування відбувається за неспаданням (reverse=False).  Для сортування за незростанням слід задати значення reverse=True, або після сортування за замовчуванням  застосувати метод reverse().
Щоб зрозуміти сутність алгоритмів сортування, розглянемо два найпростіші методи сортування масиву. Нехай потрібно впорядкувати елементи списку arr із 10 елементів за неспаданням:
arr[1] ≤ arr[2] ≤ ... ≤ arr[10]

Алгоритм сортування вибором максимального елемента

Поки довжина неупорядкованої частини списку більше 1, повторювати:

• знайти в неупорядкованому зрізі списку максимальне значення;
• поміняти місцями  максимальне значення з останнім елементом неупорядкованого зрізу;
• зменшити довжину  неопрацьованого зрізу на один елемент.

 

 

Реалізуємо алгоритм у вигляді функції. Список arr заповнимо 10 випадковими числами.

 

from random import randint
def sort_select():	# Заголовок функції сортування
for k in range(len(arr)–1, 0, –1):	# При кожній ітерації циклу переглядається зріз [0: k+1]
mk = max(arr[0: k+1])	# Знайшли максимальний елемент у зрізі arr[0: k+1]
m = arr[0: k+1].index(mk)	# Визначили індекс максимального елемента
arr[k], arr[m] = arr[m], arr[k]	# Максимальний елемент поміняли місцями з останнім у зрізі
Основна програма
arr = [] for i in range(10):                arr.append(randint(1, 30))	# Заповнення списку випадковими числами
print(arr)	# Виведення початкового списку
sort_select()	# Виклик функції сортування
print(arr)	# Виведення упорядкованого списку

У процесі виконання цього алгоритму елементи з великими значеннями опиняються в кінці списку, а елементи з меншими значеннями поступово переміщуються у напрямку до початку списку. Образно кажучи, важкі елементи падають на дно, а легкі повільно спливають подібно до бульбашок повітря.

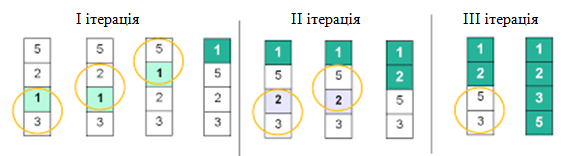
Розглянемо сортування масиву arr=[3,1,2,5] за спаданням. Переглядаємо частини списку довжиною k = 4..2.

 

І ітерація. Довжина неупорядкованої частини списку k = 4. 

• 3<1? Ні.
• 1<2? Так. 1 і 2 міняємо місцями.
• 1<5? Так. 1 i 5 міняємо місцями.

Для скорочення числа ітерацій зовнішнього циклу можна ввести  допоміжну змінну prap типу bool, яка виконує роль прапорця. Вона отримує значення True в тому випадку, якщо відбулася хоча б одна перестановка сусідніх елементів. Якщо значення рrap не змінилось, це означає, що елементи списку вже впорядковані й подальший перегляд списку не потрібний.

Реалізуємо алгоритм у вигляді функції.
def sort_bulb():
       prap = True
       k = len(arr)–1
       while prap:
             prap = False
             for i in range(k):
                     if arr[i]<arr[i+1]:
                           arr[i], arr[i+1] = arr[i+1], arr[i]
                           prap = True
            k = k–1

Для різних наборів значень списку може знадобитися різна кількість кроків сортування.