Під час опрацювання таблиць часто виникає потреба впорядкувати дані в таблиці за деякою ознакою. Числові дані можна відсортувати за величиною (наприклад, розташування в масиві значень вартості товарів за зростанням), рядкові дані — в алфавітному порядку (упорядкування списку учнів).
Сортування елементів масиву — це розстановка елементів масиву в заданому порядку (за зростанням, за зменшенням, за останньою цифрою, в лексикографічному порядку тощо).
Навіщо потрібне сортування?
З відсортованими даними працювати легше, ніж з довільно розташованими:
- коли елементи відсортовані, їх простіше знайти;
- на відсортованих даних легше визначити, чи є пропущені елементи;
- простіше упевнитися, що всі елементи були перевірені;
- легше знайти спільні елементи двох множин.
Сортування є потужним засобом прискорення роботи практично будь-якого алгоритму, в якому потрібно часто звертатися до певних елементів даних.
Розглянемо два найпростіші методи сортування масиву.
Сортування вибором максимального елемента
Нехай потрібно впорядкувати масив X: аrray[1..10] оf Real; за неспаданням:
X[1] ≤ X[2] ≤ ... ≤ X[10].
Алгоритм сортування:
• Відшукати максимальний елемент з послідовності X[1]..X[10].
• Максимальний елемент із цієї послідовності поміняти місцями з X[10].
• Відшукати максимальний елемент із послідовності X[1]..X[9].
• Максимальний елемент із цієї послідовності поміняти місцями з X[9].
<…>
• Максимальний елемент із послідовності X[1]..X[2] поміняти місцями з X[2].
• Відшукати максимальний елемент з послідовності X[1]..X[10].
• Максимальний елемент із цієї послідовності поміняти місцями з X[10].
• Відшукати максимальний елемент із послідовності X[1]..X[9].
• Максимальний елемент із цієї послідовності поміняти місцями з X[9].
<…>
• Максимальний елемент із послідовності X[1]..X[2] поміняти місцями з X[2].
Приклад:
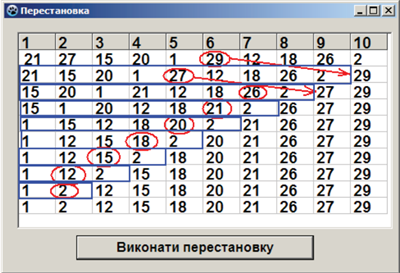
Проаналізуй вигляд масиву X[1..10] на кожному кроці сортування
за неспаданням вибором максимального елемента.
за неспаданням вибором максимального елемента.
Програмний код, що реалізує описаний алгоритм:
For K := 10 downto 2 do
begin { пошук М — номера Мах(X[1..K])}
M := 1; Max := X[1];
For i := 2 to K do
If [Xi] > Max Then begin
Max := X[i]; M := i; end;
{ перестановка X[K] і X[M] }
C := X[M]; X[M] := X[K]; X[K] := C;
end;
begin { пошук М — номера Мах(X[1..K])}
M := 1; Max := X[1];
For i := 2 to K do
If [Xi] > Max Then begin
Max := X[i]; M := i; end;
{ перестановка X[K] і X[M] }
C := X[M]; X[M] := X[K]; X[K] := C;
end;
Сортування обміном (метод бульбашки)
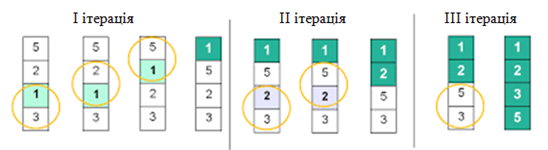
Метод бульбашки ґрунтується на порівнянні та перестановці сусідніх чисел.
Алгоритм сортування:
• Послідовно порівнювати пари сусідніх елементів X[і] і X[і+1] (і:1..N–1), і, якщо X[і] > X[і+1], то поміняти їх місцями, логічній змінній Prap надати значення True. У результаті першого перегляду послідовності на N—му місці буде найбільший з усіх елементів, тобто він, як бульбашка, «спливе» вгору.
• Переглянути елементи від 1 до N–2; на (N–1)му місці з’явиться найбільший серед (N–1) перших елементів і т. д.
Алгоритм сортування:
• Послідовно порівнювати пари сусідніх елементів X[і] і X[і+1] (і:1..N–1), і, якщо X[і] > X[і+1], то поміняти їх місцями, логічній змінній Prap надати значення True. У результаті першого перегляду послідовності на N—му місці буде найбільший з усіх елементів, тобто він, як бульбашка, «спливе» вгору.
• Переглянути елементи від 1 до N–2; на (N–1)му місці з’явиться найбільший серед (N–1) перших елементів і т. д.
Програмний код, що реалізує описаний алгоритм:
Repeat
Prap := False;
For i := 1 to 9 do
If X[i] > X[i+1] Then begin
C := X[i];
For i := 1 to 9 do
If X[i] > X[i+1] Then begin
C := X[i];
X[i] := X[i+1];
X[i+1] := C;
Prap := True end
Until Prap = False;
Prap := True end
Until Prap = False;
Змінна Prap: Boolean виконує роль прапорця. Вона отримує значення True в тому випадку, якщо відбулась хоча б одна перестановка сусідніх елементів. Якщо значення Prap не змінилось, це означає, що елементи масиву вже впорядковані і подальший перегляд послідовності значень не потрібний.