Одна з найдавніших математичних наук — геометрія. Це вивчення фігур, їх властивостей і взаємного розташування.
Перші геометричні факти знайдені у вавилонських клинописних таблицях і єгипетських папірусах (III тисячоліття до нашої ери), а також в інших джерелах. Сама назва науки давньогрецького походження. Назви багатьох фігур походять з грецької та латинської (Стародавній Рим) мов.
Для створення фігур будемо використовувати точки і прямі. За допомогою цих фігур ми визначимо всі інші геометричні фігури, а точку і пряму спробуємо уявити: точку — як щось нескінченно маленьке, а пряму — як щось, що нескінченно простягається в обидві сторони.
Точки позначаються великими латинськими літерами, прямі позначаються однією маленькою латинською літерою або двома великими латинськими літерами. Словами описати взаємне розташування точок і прямої можна так:
- точка знаходиться (лежить) на прямій або пряма проходить (проведена) через точку;
- точка не знаходиться (не лежить) на прямій або пряма не проходить (не проведена) через точку.
Частина прямої, обмежена двома точками і точки, називають відрізком.
Частина прямої, обмежена однією точкою і точку, називають променем.
Промені зі спільною початковою точкою на одній прямій називають додатковими або протилежними.
Для назви відрізка послідовність літер не має значення, тобто, відрізок \(AB\) той же відрізок \(BA\).
Для назви променя важливо, щоб початкова точка променя була першою літерою цієї назви.
Приклад:
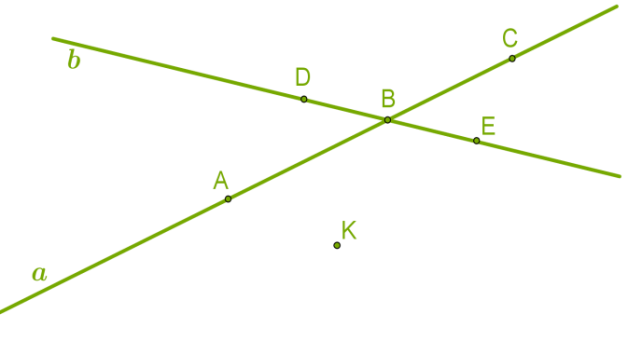
Опис малюнка:
-
намальовані прямі \(a\) і \(b\), можна сказати, також прямі \(AC\) і \(DE\);
-
дані прямі також проходять через точку \(B\), вони перетинаються в цій точці;
-
точка \(K\) не знаходиться ні на одній прямій, тобто дані прямі не проходять через цю точку;
-
на прямій \(a\) знаходяться відрізки \(AC\), \(AB\), \(BC\), у відрізків\(AB\) і \(BC\) спільна кінцева точка\(B\);
-
протилежні промені \(BA\) і \(BC\) знаходяться на прямій \(a\), протилежні промені \(BD\) і \(BE\) знаходяться на прямій \(b\).

Властивості прямих, променів і відрізків:
1. через дві точки можна провести тільки одну пряму.
2. дві прямі можуть перетинатися тільки в одній точці.
3. відрізки рівні, якщо мають однакову довжину.