Зайдемо значення виразу \(14 + 2\). Розглянемо малюнок.
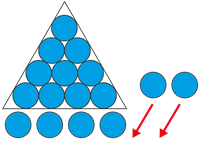
Було \(14\). \(14\) — це \(1\) десяток і \(4\) одиниці.
До \(14\) додали ще \(2\), отже \(2\) одиниці приєднали — додали до \(4\) одиниць, одержали \(6\) одиниць. Маємо \(1\) десяток і \(6\) одиниць — це число \(16\):
\(14 + 2 = 16\)
Розглянемо, як виконали додавання чисел \(16 + 3\):
Перший доданок — число \(16\) — подаємо у вигляді суми розрядних доданків: \(16 = 10 + 6.\)
До суми \(10\) і \(6\) треба додати \(3\). Додаємо \(3\) одиниці до \(6\) одиниць: \(6 + 3 = 9.\)
До \(10\) додаємо одержане число \(9\): \(10 + 9 = 19\).
Виконаємо розгорнутий запис:
\(16 + 3 = (10 + 6) + 3 = 10 + ( 6 + 3 ) = 10 + 9 = 19\)
Додавання одноцифрового числа до двоцифрового без переходу через розряд виконуй за алгоритмом:
1) Двоцифрове число замінюю сумою десятків та одиниць.
2) Додаю одиниці до одиниць.
3) До десятків додаю одержаний результат.