2. Задачі на знаходження четвертого пропорційного (два способи розв'язання)

 

Існує два способи розв’язування деяких задач на знаходження четвертого пропорційного.

 

Максимко купив \(8\) ручок і \(4\) маркери за однаковою ціною. За ручки він заплатив \(24\) грн. Скільки гривень заплатив Максимко за маркери?

 

 

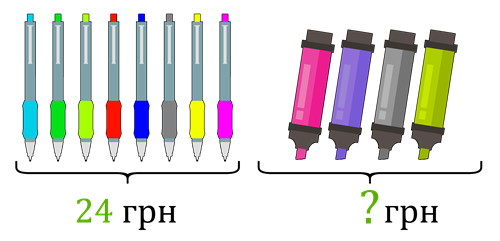
Складемо короткий запис до задачі.

 

 

Коротко задачу можна зобразити у вигляді таблиці.

 

 

\(I\) спосіб

зведення до \(1\) (\(одиниці\))

 

1) $24 : 8 = 3$ \((грн)\) — ціна однієї ручки;

 

За умовою ціна ручки і маркера однакова. Отже, знайдемо вартість \(4\) маркерів по \(3\) грн.

 

2) $3 \cdot 4 = 12$ \((грн)\)

 

Складемо вираз.

 

$(24 : 8) \cdot 4 = 12$ \((грн)\)

 

\(II\) спосіб

(\(спосіб\) \(відношення\))

 

У скільки разів менше маркерів, ніж ручок, купив Максимко, у стільки ж разів менше він заплатив за них.
У першій дії знайдемо у скільки разів менше маркерів, ніж ручок.

 

1) $8 : 4 = 2$ \((рази)\);

 

Щоб знайти вартість у \(2\) рази менше, потрібно виконати дію ділення.

 

2) $24 : 2 = 12$ \((грн)\)

 

Складемо вираз.

$24 :\; (8 : 4)\; = 12$ \((грн)\)

Відповідь: Максимко заплатив за маркери \(12\) гривень.