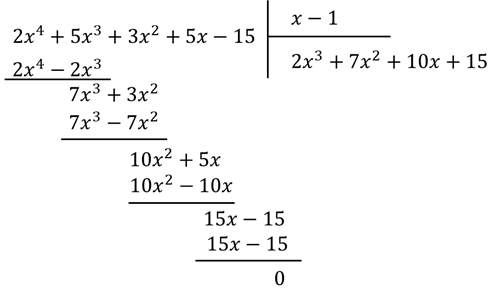2. Рівняння вищих степенів та їхні розв'язки

Двочленні рівняння.

Двочленними називають рівняння виду

x^{n} - a = 0 (n \in N) .

Якщо \(n\) — парне рівняння може мати два корені, один або жодного.

\begin{array}{l} x^{4} = 35, \Rightarrow x_{1,2} = \pm \sqrt[4]{35} . \\ x^{12} = 0, \Rightarrow x = 0 . \\ x^{8} = - 12, x \in \emptyset . \end{array}

Якщо \(n\) — непарне рівняння має один корінь.

\begin{array}{l} x^{7} = 17, \Rightarrow x = \sqrt[7]{17} . \\ x^{11} = - 9, \Rightarrow x = - \sqrt[11]{- 9} . \end{array}

Цілі раціональні рівняння вищих степенів.

До цієї групи рівнянь відносять рівняння виду

a_{0} x^{n} + a_{1} x^{n - 1} + a_{2} x^{n - 2} + ... + a_{n - 1} x + a_{n} = 0, де n \in N i n > 2 .

Рівняння даної групи розв'язують за алгоритмом:

— знайди множину дільників вільного члена

a_{n}

;

— перевір, які з дільників є коренями многочлена

P_{n} (x) = 0

, використовуючи теорему Безу;

— виконай ділення

P_{n} (x) : (x - x_{n}) де x_{n}

— корінь

P_{n} (x) = 0

Приклад:

\begin{array}{l} 2 x^{4} + {5x}^{3} + 3 x^{2} + 5x - 15 = 0 . \\ Випиши всі дільники вільного члена (- 15) : \pm 1; \pm 3; \pm 5; \pm 15 . \\ Перевір дільники : \\ P (- 1) = 2 \cdot {(- 1)}^{4} + 5 \cdot {(- 1)}^{3} + 3 \cdot {(- 1)}^{2} + 5 \cdot (- 1) - 15 \neq 0, \\ P (1) = 2 \cdot {(1)}^{4} + 5 \cdot {(1)}^{3} + 3 \cdot {(1)}^{2} + 5 \cdot (1) - 15 = 0 . \\ x_{1} = 1 - корінь . \\ Виконай ділення P (x) : (x - 1) . \end{array}

\begin{array}{l} 2 x^{4} + 5 x^{3} + 3 x^{2} + 5 x - 15 = (x - 1) \cdot (2 x^{3} + 7 x^{2} + 10 x + 15) . \\ Застосуй алгоритм для многочлена B (x) = 2 x^{3} + 7 x^{2} + 10 x + 15 . \\ Другий корінь рівняння x_{2} = - 2.7 . \\ Більше коренів дане рівняння не має . \end{array}

Знайшли помилку?