Побудуємо графік функції \(,\) і на його прикладі розглянемо властивості функції кореня \(n\)-го степеня, де \(n\) — непарне число \((3, 5, 7 … ).\)
Для побудови графіка при заповнимо таблицю.
\(x\) | \(0\) | \(1\) | ||
\(y\) | \(0\) | \(1\) |
Позначимо отримані точки на координатній площині та з'єднаємо їх плавною кривою, потім до побудованої вітки додамо вітку, симетричну їй відносно початку координат.
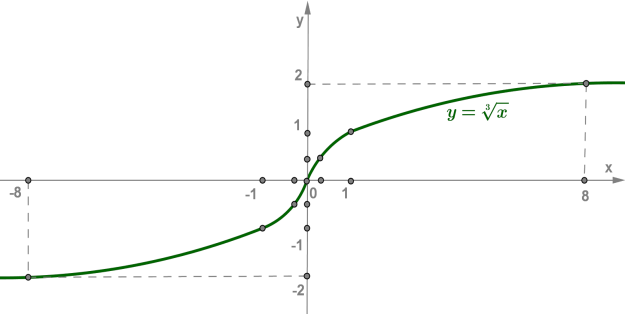
Якщо \(n\) — непарне число, то графік функції має вигляд, як на рисунку:
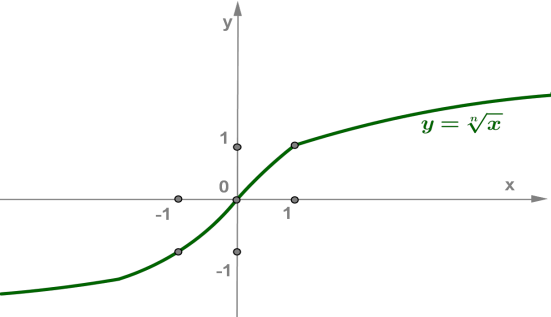
Властивості функції \(,\) де \(n\) — непарне число
\(1.\) Область визначення \(.\)
\(2.\) Область значень \(.\)
\(3.\) Зростає при \(.\)
\(4.\) Не має найбільшого і найменшого значень.
\(5.\) Необмежена зверху і знизу.
\(6.\) Неперервна.
\(6.\) Неперервна.
\(7.\) Опукла вгору на промені \(,\) опукла вгору на промені \(.\)
\(8.\) Непарна.
