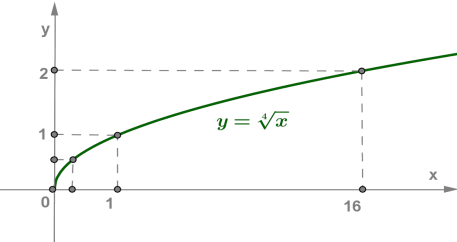
Побудуємо графік функції \(,\) і на його прикладі розглянемо властивості функції кореня \(n\)-го степеня, де \(n\) — парне число \((\)\(2, 4, 6\) … \().\)
Для побудови графіка при заповнимо таблицю.
\(x\) | \(0\) | \(1\) | ||
\(y\) | \(0\) | \(1\) |
Позначимо отримані точки на координатній площині і з'єднаємо їх плавною кривою.
Якщо \(n\) — парне число, то графік функції має вигляд, як на рисунку:
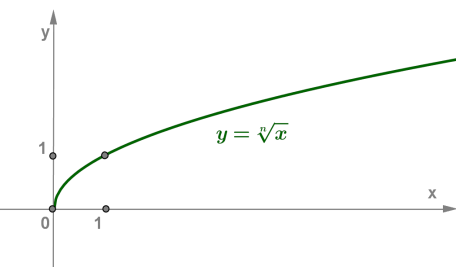
Властивості функції \(,\) де \(n\) — парне число
\(1.\) Область визначення \(.\)
\(2.\) Область значень \(.\)
\(3.\) Зростає при \(.\)
\(4.\) Не має найбільшого значення.
\(5.\) \(.\)
\(6.\) Необмежена зверху, обмежена знизу.
\(7.\) Неперервна.
\(7.\) Неперервна.
\(8.\) Опукла вгору на промені \(.\)
\(9.\) Диференційована в будь-якій точці \(х>0.\)
\(10.\) Ні парна, ні непарна.