Степенева функція з натуральним показником

Функція вигляду

y = x^{n}, де n = 1, 2, 3, 4, 5, ...

називається cтепеневою функцією з натуральним показником.

Функція

y = x^{4}, x \geq 0

Складемо таблицю значень для цієї функції:

$x$	$0$	$1$	$\frac{1}{2}$	$\frac{3}{2}$
$y$	$0$	$1$	$\frac{1}{16}$	$\frac{81}{16}$

Побудуємо точки

(0; 0)

$,$

(1; 1)

$,$

(\frac{1}{2}; \frac{1}{16})

$,$

(\frac{3}{2}; \frac{81}{16})

на координатній площині.

Дані точки намічають деяку лінію, проведемо її.

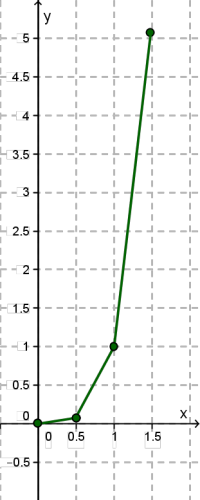
Додамо до даного графіка лінію, симетричну побудованій відносно осі ординат.

Отримаємо графік функції

y = x^{4}, x \in (- \infty; + \infty)

$.$

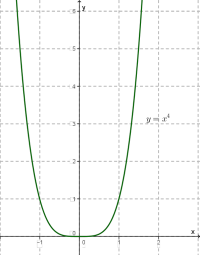
Зверни увагу!

Графік схожий на параболу, але параболою його не називають.

Властивості функції

y = x^{4}

$1.$

D (f) = (- \infty; + \infty)

$.$

$2.$ Парна.

$3.$ Спадає на промені

(- \infty; 0]

$,$ зростає на промені

[0; + \infty)

$.$

$4.$ Обмежена знизу, необмежена зверху.

$5.$

y_{найм} = 0; y_{найб}

не існує.

$6.$ Неперервна.

$7.$

E (f) = [0; + \infty)

$.$

$8.$ Опукла вниз.

Функція

y = x^{3}

Функція

y = x^{3}

— непарна, отже, її графік симетричний відносно початку координат.

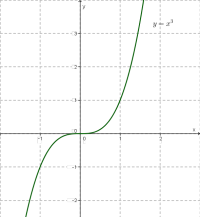
Графік функції

y = x^{3}

при

x \geq 0

виглядає так само, як графік функції

y = x^{4}

при

x \geq 0

$.$ Потрібно лише врахувати, що нова крива трохи менш круто йде вгору і трохи далі віддалена від осі $x$ біля початку координат. Додавши лінію, симетричну побудованій, відносно початку координат, отримаємо графік функції

y = x^{3}

$.$

Зверни увагу!

Криву називають кубічною параболою.

Зазначимо деякі геометричні особливості кубічної параболи

y = x^{3}

$.$

У неї є центр симетрії — точка $(0;0),$ яка відокремлює одну від одної дві симетричні частини кривої. Ці симетричні частини називаються гілками кубічної параболи.