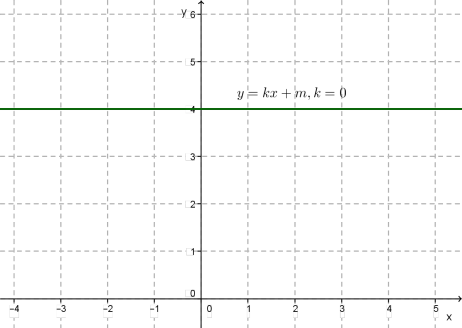
Лінійна функція
Зверни увагу!
Графіком функції є пряма.
\(1)\) \(;\)
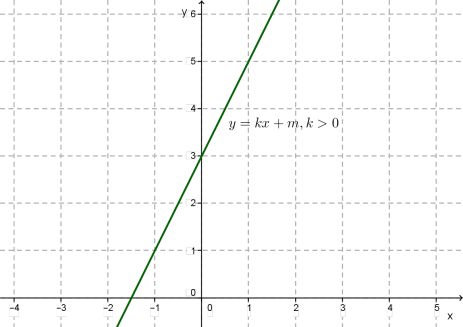
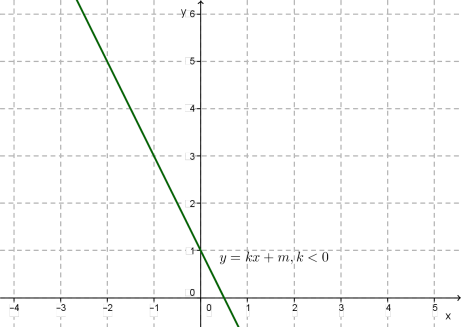
\(2)\) зростає, якщо \(k > 0\) та спадає, якщо \(k < 0;\)
\(3)\) необмежена ні знизу, ні зверху;
\(4)\) не має ні найбільшого, ні найменшого значень;
\(5)\) неперервна;
\(6)\) \(.\)
Функція
Зверни увагу!
Графіком функції є парабола з вершиною на початку координат і з вітками, напрямленими вгору, якщо \(k > 0\) та вниз, якщо \(k < 0.\)
Для випадку \(k > 0\)\(:\)
\(1)\) \(;\)
\(2)\) спадає на промені \(,\) зростає на промені \(;\)
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) \(,\) найбільшого не існує;
\(5)\) неперервна;
\(5)\) неперервна;
\(6)\) \(;\)
\(7)\) опукла вниз.
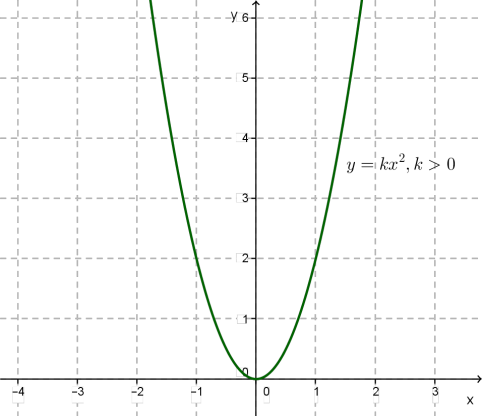
Властивості функції
Для випадку \(k < 0\)\(:\)
\(1)\) \(;\)
\(2)\) зростає на промені \(,\) спадає на промені \(;\)
\(3)\) необмежена знизу, обмежена зверху;
\(4)\) найменшого значення не існує, \(;\)
\(4)\) найменшого значення не існує, \(;\)
\(5)\) неперервна;
\(6)\) \(;\)
\(7)\) опукла вгору.
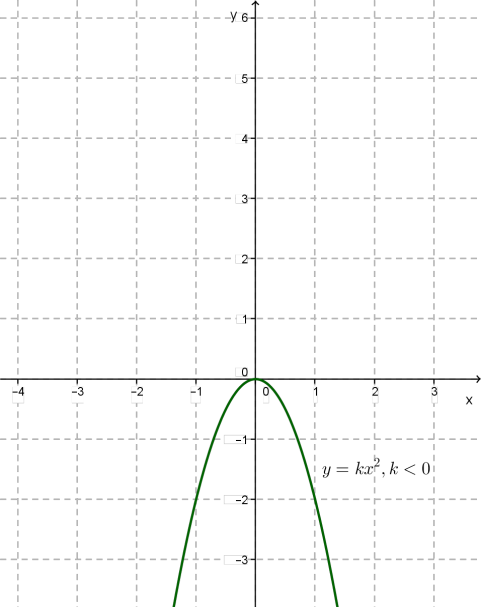
Функція
Зверни увагу!
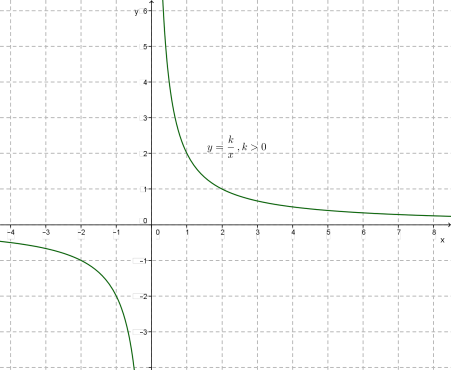
Графіком функції є гіпербола.
Властивості функції
\(1)\) \(;\)
\(2)\) якщо \(k> 0,\) то функція спадає на відкритому промені та на відкритому промені \(;\) якщо \(k<0,\) то функція зростає на та на \(;\)
\(3)\) необмежена ні знизу, ні зверху;
\(4)\) не має ні найбільшого, ні найменшого значень;
\(5\) неперервна на відкритому промені та на відкритому промені \(;\)
\(4)\) не має ні найбільшого, ні найменшого значень;
\(5\) неперервна на відкритому промені та на відкритому промені \(;\)
\(6)\) \(.\)
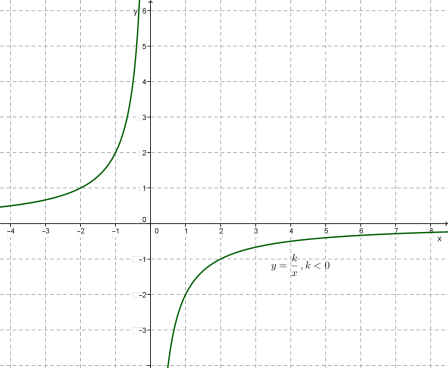
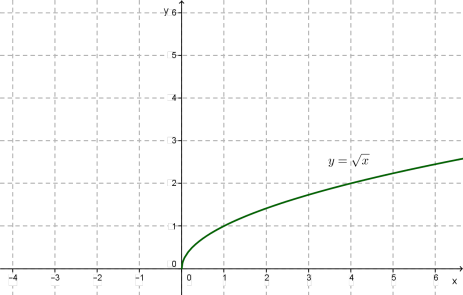
Функція
Зверни увагу!
Графіком функції є вітка параболи.
\(1\) \(;\)
\(2)\) зростає;
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) \(,\) найбільшого не існує;
\(5)\) неперервна;
\(5)\) неперервна;
\(6)\) \(;\)
\(7)\) опукла вгору.
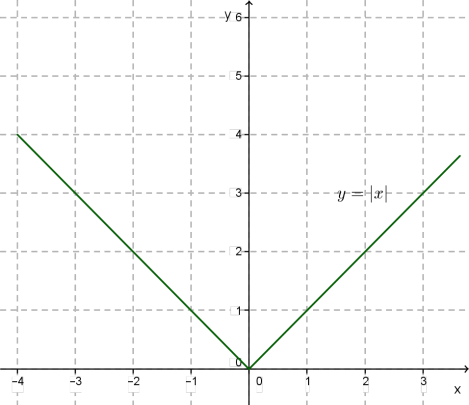
Функція
Зверни увагу!
Графіком функції є об'єднання двох променів: та \(.\)
\(1)\) \(;\)
\(2)\) спадає на промені \(,\) зростає на промені \(;\)
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) \(,\) найбільшого не існує;
\(5)\) неперервна;
\(6)\) \(.\)
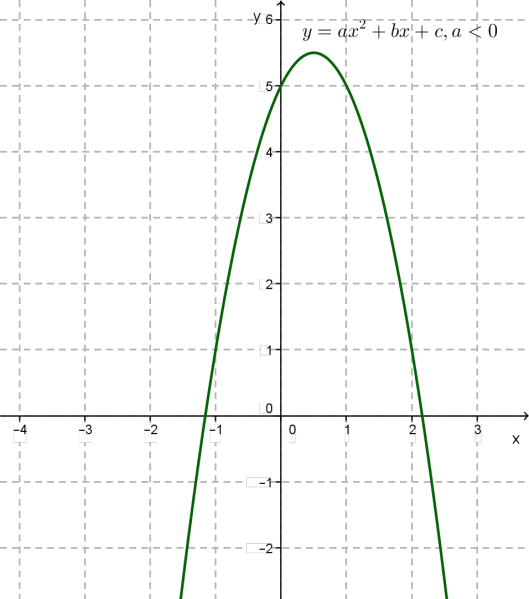
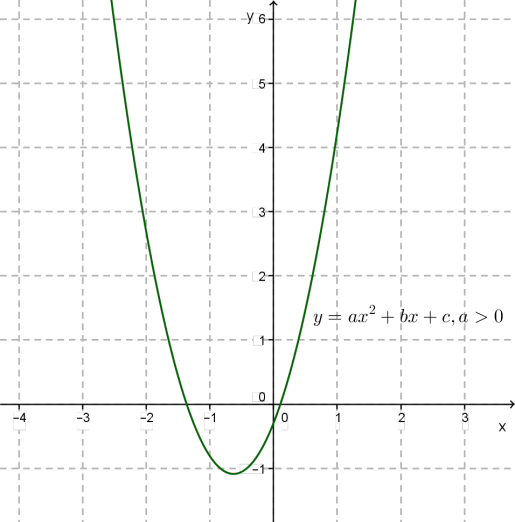
Функція
Зверни увагу!
Графіком функції є парабола з вершиною в точці \(,\) де \(,\) і з вітками, напрямленими вгору, якщо \(a > 0\) та вниз, якщо \(a < 0.\)
Властивості функції
Для випадку \(a > 0\)\(:\)
\(1)\) \(;\)
\(2)\) спадає на промені \(,\) зростає на промені \(;\)
\(3)\) обмежена знизу, необмежена зверху;
\(4)\) \(,\) найбільшого не існує;
\(5)\) неперервна;
\(6)\) \(;\)
\(7)\) опукла вниз.
Для випадку \(a < 0\)\(:\)
\(1)\) \(;\)
\(2)\) зростає на промені \(,\) спадає на промені \(;\)
\(3)\) необмежена знизу, обмежена зверху;
\(4)\) найменшого значення не існує, \(;\)
\(5)\) неперервна;
\(6)\) \(;\)
\(7)\) опукла вгору.