Теорема 3. Якщо функція \(y=f(x)\) має екстремум в точці , тоді в цій точці похідна функції або дорівнює нулю, або не існує.
Теорема 4 (достатні умови екстремуму). Нехай функція неперервна на проміжку \(X\) і має всередині проміжку стаціонарну або критичну точку . Тоді:
а ) якщо у цієї точки існує такий окіл, в якому при виконується нерівність , а при — нерівність , тоді — точка мінімуму функції );
б ) якщо у цієї точки існує такий окіл, в якому при виконується нерівність , а при — нерівність , тоді — точка максимуму функції ) ;
в) якщо у цієї точки існує такий окіл, що в ньому і ліворуч і праворуч від точки знаки похідної однакові, тоді в точці экстремума немає.
Для зручності домовимося внутрішні точки області визначення функції, в яких похідна функції дорівнює нулю, називати стаціонарними, а внутрішні точки області визначення функції, в яких функція неперервна, але похідна не існує, — критичними.
Отже, щоб визначити екстремуми (мінімуми і максимуми) функції , спочатку потрібно знайти критичні точки, в яких або ж похідна не існує (і які належать області визначення функції). Тоді легко визначити інтервали, в яких у похідної незмінний знак. (Критичні (стаціонарні) точки ділять реальну числову пряму на інтервали з незмінним знаком похідної. Щоб визначити знак похідної, достатньо обчислити значення похідної функції в будь-якій точці відповідного інтервалу).
Алгоритм дослідження неперервної функції на монотонність і екстремуми:
1. знайти похідну .
2. знайти стаціонарні та критичні .
3. відзначити стаціонарні та критичні точки на числовій прямій і визначити знаки похідної на одержаних проміжках.
4. спираючись на теореми 1, 2 і 4, зробити висновки про монотонності функції і про її точки екстремуму.
Отже: якщо похідна функції в критичній точці:
1) змінює знак з від'ємного на додатний, тоді це точка локального мінімуму;
2) змінює знак з додатного на від'ємний, тоді це точка локального максимуму;
3) не змінює знак, тоді в цій точці немає екстремуму.
+ | - | - | + |
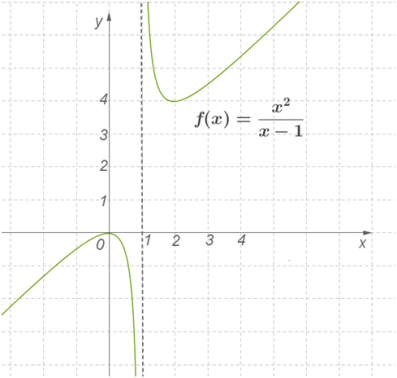
У точці \(x=0\) вона змінює знак з додатного на від'ємний, отже, це точка локального максимуму зі значенням функції \(f(0)=0\).
У точці \(x=2\) вона змінює знак з від'ємного на додатний, отже, це точка локального мінімуму зі значенням функції \(f(2)=4\).