1. Дослідження функцій на монотонність

Теорема 1. Якщо у всіх точках відкритого проміжку \(X\) виконується нерівність f′(x)≥0 (причому рівність f′(x)=0 виконується лише в окремих точках і не виконується ні на якому суцільному проміжку), тоді функція y=f(x)) зростає на проміжку \(X\).

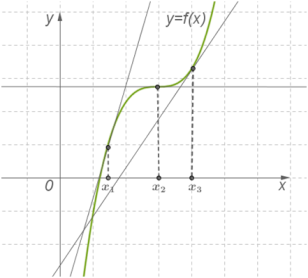
augoša funk..bmp

Теорема 2. Якщо у всіх точках відкритого проміжку \(X\) виконується нерівність f′(x)≤0 (причому рівність f′(x)=0 виконується лише в окремих точках і не виконується ні на якому суцільному проміжку), тоді функція y=f(x) спадає на проміжку\(X\).

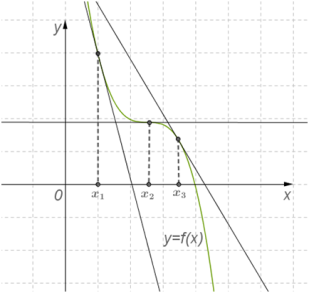
dilst_funk.bmp

Отже:
якщо існує похідна функції в інтервалі \((a, b)\) і в даному інтервалі
1) f′(x)≥0, тоді функція в ньому не спадає;
2) f′(x)≤0, тоді функція в ньому не зростає;
3) f′(x)>0, тоді функція в ньому зростає;
4) f′(x)<0, тоді функція в ньому спадає.
 
Приклад:
Необхідно досліджувати інтервали монотонності функції f(x)=x3−4x2−16x+17.
 
Спочатку знаходимо похідну: f′(x)=(x3−4x2−16x+17)′=3x2−8x−16.
Це парабола, яка перетинає вісь x в точках x1=−43 і x2=4 і її гілки спрямовані вгору. Тому похідна від'ємна в інтервалі −43;4 (функція спадає) і додатна в інтервалах −∞;−43 і (4;+∞) (функція зростає).
 
Відповідь: 
функція f(x)=x3−4x2−16x+17 зростає в інтервалах −∞;−43 і (4;+∞), спадає в інтервалі −43;4.
Попередня тема
Повернутись до теми
Наступна теорія
Copyright © 2024 МiйКлас