Завдання на відшукання найбільших і найменших значень величин

Російський математик XIX століття П. Л. Чебишев казав, що «особливу важливість мають ті методи науки, які дозволяють розв'язувати задачу, загальну для всієї практичної діяльності людини: як мати у розпорядженні свої засоби для досягнення найбільшої вигоди."
Завдання подібного роду носять спільну назву — задачі на оптимізацію (от латинського слова optimum — «найкращий»).

Завдання на оптимізацію розв'язують за звичайною схемою з трьох етапів математичного моделювання:

1. утворення математичної моделі;

2. робота з моделлю;

3. відповідь на питання завдання.

Далі рекомендації методичного плану.

Перший етап. Утворення математичної моделі.

1. Проаналізувавши умови задачі, виділяємо величину, яка оптимізується (скорочено: $О. В.$), тобто величину, про найбільше або найменше значення якої йдеться. Позначаємо її буквою $y$ (або $S, V, R, t$ - залежно від фабули).

2. Одну з тих, що беруть участь в задачі невідомих величин, через яку порівняно неважко виразити $О. В.$, приймаємо за незалежну змінну (скорочено: $Н. З.$) і позначаємо її буквою $x$ (або якою-небудь іншою буквою). Встановлюємо реальні границі зміни $Н. З.$ (відповідно до умов задачі), тобто область визначення для шуканої $О. В.$

3. Виходячи з умов завдання, висловлюємо $y$ через $x$. Математична модель задачі являє собою функцію $y=f(x)$) з областю визначення $X$, яку знайшли на другому кроці.

Другий етап. Робота зі складеною моделлю.

На цьому етапі для функції $y=f(x)$, $x \in X$ знаходимо $y_{найм}$ або $y_{найб}$ , в залежності від того, що потрібно в умові завдання. При цьому використовуються теоретичні установки, які були дані в першому пункті даного параграфа.

Третій етап. Відповідь на питання завдання.

Тут слід дати конкретну відповідь на питання завдання, спираючись на результати, отримані на етапі роботи з моделлю.

Приклад:

Міцність балки прямокутного перетину пропорційна добутку її ширини на квадрат висоти. Який перетин повинна мати балка, витесана з циліндричної колоди радіуса $R$, щоб її міцність була найбільшою?

Розв'язання. Перший етап. Утворення математичної моделі.

1. Оптимізована величина (О. В.) - міцність балки, оскільки в задачі потрібно з'ясувати, коли міцність балки буде найбільшою. Позначимо О. В. буквою $y$.

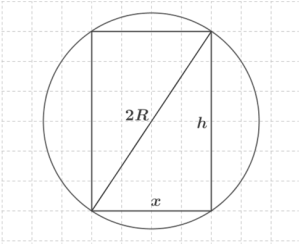
2. Міцність залежить від ширини і висоти прямокутника, що служить осьовим перерізом балки. Оголосимо незалежною змінною (Н. П.) ширину балки, позначимо її буквою $x$. Оскільки осьовий переріз являє собою прямокутник, вписаний в коло радіуса $R$ (див.рис.), тоді $0<x<2R$ - такі реальні границі зміни незалежної змінної.

3. Висота $h$ прямокутника пов'язана з його шириною співвідношенням $x^{2} + h^{2} = 4 R^{2}$ (за теоремою $Піфагора$). Отже, $h^{2} = 4 R^{2} - x^{2}$ .

Міцність балки $y$ пропорційна добутку ${xh}^{2}$ , тобто ${y = kxh}^{2}$ (де коефіцієнт $k$ — деяке додатне число).
Отже,
$y = kx (4 R^{2} - x^{2}), x \in (0; 2 R)$ .

Математична модель задачі утворена.

Другий етап. Робота зі складеною моделлю.
На цьому етапі для функції $y = kx (4 R^{2} - x^{2}), x \in (0; 2 R)$ треба знайти $y_{найб}$ .

Маємо:

$\begin{array}{l} y = 4kx R^{2} - k x^{3}; \\ y^{'} = 4k R^{2} - 3 k x^{2} . \end{array}$

Критичних точок немає. Знайдемо стаціонарні точки. Прирівнявши похідну до нуля, отримаємо:

$\begin{array}{l} 4k R^{2} - 3 k x^{2} = 0 \\ x_{1} = \frac{2 R}{\sqrt{3}}; x_{2} = - \frac{2 R}{\sqrt{3}} . \end{array}$

Заданому інтервалу $(0; 2R)$ належить лише точка $x_{1}$ і причому $x_{1} = \frac{2 R}{\sqrt{3}}$ — точка максимуму функції. Отже, за теоремою з пункту 1,

$y_{найб} = f (x_{1}) = f (\frac{2 R}{\sqrt{3}}) = \frac{16 k R^{3}}{3 \sqrt{3}}$ .

Третій етап. Відповідь на питання завдання.

У задачі питається, який перетин повинна мати балка найбільшої міцності. Ми з'ясували, що ширина $x$ прямокутника, що служить осьовим перерізом найбільш міцної балки, дорівнює $\frac{2 R}{\sqrt{3}}$ . Знайдемо висоту:

$\begin{array}{l} h^{2} = 4 R^{2} - \frac{4 R^{2}}{3} = \frac{8 R^{2}}{3} \\ h = \frac{2 R \sqrt{2}}{\sqrt{3}} \Rightarrow \frac{h}{x} = \sqrt{2} . \end{array}$

Відповідь: перетином балки повинен служити прямокутник, у якого відношення висоти до ширини дорівнює $\sqrt{2}$ .

Зауваження. Кваліфіковані майстри приходять до такого ж результату, спираючись на свій досвід, але, зрозуміло, вони приймають вказане відношення рівним $1,4$ ( $\sqrt{2} \approx 1.4$ ).

Попередня теорія

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!

2. Завдання на відшукання найбільших і найменших значень величин

Теорія: