Для знаходження найбільшого і найменшого значень функції найчастіше використовується графік функції. У деяких випадках можна знайти найбільше і найменше значення функції і без допомоги графіка, використовуючи міркування. У більш складних випадках використовується похідна. Для цього сформулюємо деякі теореми.
1. Якщо функція неперервна на відрізку, тоді вона досягає на ньому і свого найбільшого, і свого найменшого значень (ця теорема доводиться в курсі вищої математики).
2. Найбільшого і найменшого значень безперервна функція може досягати як на кінцях відрізка, так і всередині нього.
3. Якщо найбільше (або найменше) значення досягається всередині відрізка, тоді тільки в стаціонарній або критичній точці.
Алгоритм знаходження найменшого та найбільшого значень неперервної функції \(f(x)\) на відрізку \([a; b]\):
1. Знайти похідну .
2. Знайти стаціонарні та критичні точки функції, що лежать всередині відрізка \([a; b]\).
3. Обчислити значення функції в точках, відібраних на другому кроці і в точках \(a\) і \(b\); обрати серед цих значень найменше (це буде ) і найбільше (це буде ).
А як бути, якщо мова йде про знаходження найбільшого або найменшого значення функції, неперервної на незамкнутому проміжку, наприклад на інтервалі? Можна побудувати графік функції і зняти інформацію з отриманої графічної моделі. Але частіше виявляється більш зручним використовувати наступну теорему.
Теорема. Нехай функція неперервна на проміжку \(X\) і має всередині нього єдину стаціонарну або критичну точку . Тоді:
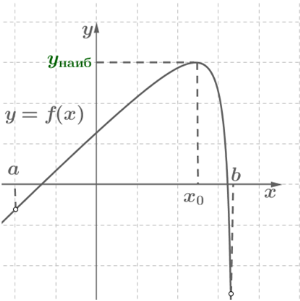
а ) якщо — точка максимуму, тоді ;
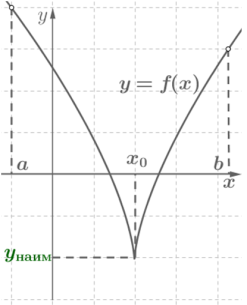
б ) якщо — точка мінімуму, тоді .
На малюнках наведені відповідні геометричні ілюстрації.