Числове коло в координатній площині

Розташуємо числове коло в координатній площини так, щоб центр кола зійшовся з початком координат, а його радіус приймаємо за одиничний відрізок.
Початкова точка числового кола $A$ поєднана з точкою $(1;0)$.

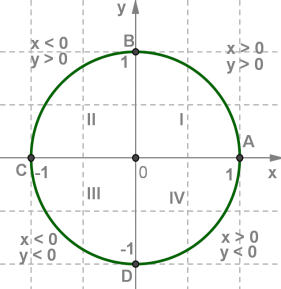
Кожна точка числового кола має в координатної площини свої координати.

Знайдемо спочатку координати тих точок координатної площини, які отримані на макетах числового кола.

Точка

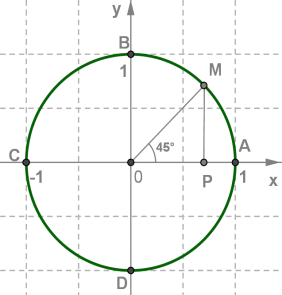M (\frac{π}{4})

середина $I$ чверті.

Опустимо перпендикуляр $MP$ на пряму $OA$ і розглянемо трикутник $OMP$.
Оскільки дуга $AM$ утворює половину дуги $AB$, тоді

∠ MOP = 45 °

Отже, трикутник $OMP$ - рівнобедрений прямокутний трикутник і $OP = MP$, тобто у точки $M$ абсциса і ордината рівні: $x = y$.

Оскільки координати точки $M (x; y)$ задовольняють рівняння числового кола

x^{2} + y^{2} = 1

тоді для їх знаходження потрібно розв'язати систему рівнянь:

\{\begin{cases} x^{2} + y^{2} = 1 \\ x = y \end{cases}

Підставивши $x$ замість $y$ в перше рівняння системи, отримаємо:

\begin{array}{l} x^{2} + x^{2} = 1 \\ 2 x^{2} = 1 \\ x^{2} = \frac{1}{2} \\ x = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \\ y = x = \frac{\sqrt{2}}{2} \end{array}

При розв'язанні враховуємо, що абсциса точки $M$ додатна.

Отримали, що координати точки $M$, яка відповідає числу

\frac{π}{4}

, будуть

M (\frac{π}{4}) = M (\frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2})

Аналогічно можна отримати координати і інших точок першого макета числового кола, враховуючи тільки знаки координат в кожній чверті.

Отримані результати запишемо в таблицю:

Точка кола.

	$0$	$\frac{π}{4}$	$\frac{π}{2}$	$\frac{3 π}{4}$	$π$	$\frac{5 π}{4}$	$\frac{3 π}{2}$	$\frac{7 π}{4}$	$2 π$
Абсциса $x$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$-1$	$- \frac{\sqrt{2}}{2}$	$0$	$\frac{\sqrt{2}}{2}$	$1$
Ордината $y$	$0$	$\frac{\sqrt{2}}{2}$	$1$	$\frac{\sqrt{2}}{2}$	$0$	$- \frac{\sqrt{2}}{2}$	$-1$	$- \frac{\sqrt{2}}{2}$	$0$

Міркуємо аналогічно для точки $M$, якщо тепер вона відповідає числу

\frac{π}{6}

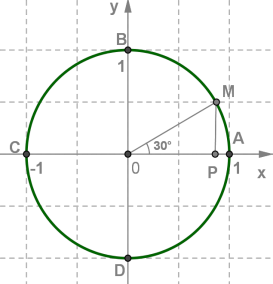Трикутник $MOP$ прямокутний. Так як дуга $AM$ складає третю частину дуги $AB$, то

∠ MOP = 30 °

Катет $MP$ лежить проти кута $30$ градусів в прямокутному трикутнику, отже, дорівнює половині гіпотенузи, тобто ордината точки $M$ дорівнює

\begin{array}{l} MP = \frac{1}{2} \\ y = \frac{1}{2} \end{array}

Абсцису $x$ точки $M$ знайдемо, розв'язавши рівняння:

x^{2} + y^{2} = 1

\begin{array}{l} x^{2} = 1 - {(\frac{1}{2})}^{2} = 1 - \frac{1}{4} = \frac{3}{4} \\ x = \frac{\sqrt{3}}{2} \end{array}

При розв'язанні враховуємо, що абсциса точки $M$ додатна.

Отримали, що координати точки $M$, яка відповідає числу

\frac{π}{6}

, будуть

M (\frac{π}{6}) = M (\frac{\sqrt{3}}{2}; \frac{1}{2})

Аналогічно можна отримати координати і інших точок другого макета числового кола, враховуючи тільки знаки координат в кожній чверті.

Отримані результати запишемо в таблицю:

Точка кола.

	$\frac{π}{6}$	$\frac{π}{3}$	$\frac{2 π}{3}$	$\frac{5 π}{6}$	$\frac{7 π}{6}$	$\frac{4 π}{3}$	$\frac{5 π}{3}$	$\frac{11 π}{6}$
Абсциса $x$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$- \frac{1}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{1}{2}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$
Ордината $y$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$- \frac{1}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{\sqrt{3}}{2}$	$- \frac{1}{2}$

Попередня теорія

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!

3. Числове коло в координатній площині

Теорія: