Числове коло.
Будь-яке коло може розглядатися, як числове, але зручніше використовувати одиничне коло.
Одиничне коло - це коло, радіус якого береться за одиницю виміру.
Вважаємо, що .
Якщо взяти , тоді довжина кола \(l\) може бути виражена числом
Будемо користуватися одиничним колом, в якому проведені горизонтальний і вертикальний діаметри \(CA\) і \(DB\) (див. рис.)
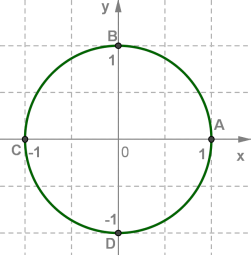
Прийнято називати дугу \(AB\) - першою чвертю, дугу \(BC\) - другою чвертю, дугу \(CD\) - третьою чвертю, дугу \(DA\) - четвертою чвертю, причому, це відкриті дуги, тобто дуги без їх кінців.
Довжина кожної чверті одиничного кола дорівнює
Прийнято в позначенні дуги на першому місці писати букву, що позначає початок дуги, а на другому місці писати букву, що позначає кінець дуги.
Для роботи з числовим колом часто використовуються два макети числового кола.
Перший макет.
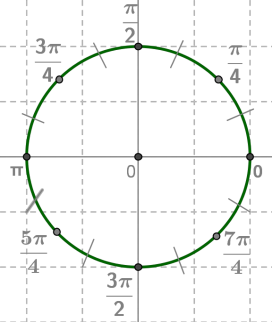
Другий макет.
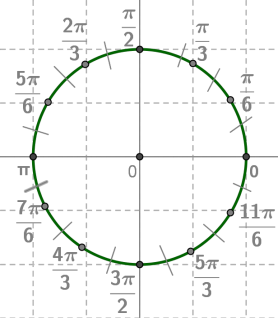
Для числового кола вірне наступне твердження:
Якщо точка \(M\) числового кола відповідає числу \(t\), тоді вона відповідає і числу виду
На зазначених двох макетах написані числа, відповідні точкам, при першому обході числового кола в додатному напрямку, тобто на проміжку
Таким чином,
одиничне коло зі встановленою відповідністю між дійсними числами і точками кола називається числовим колом.
