Функція y = tg x та її властивості — урок. Алгебра, 10 клас.

Функція

y = tg x

при

x \neq \frac{π}{2} + π n, n \in ℤ

є непарною і періодичною з періодом

π

Тому досить побудувати її графік на проміжку

[0; \frac{π}{2})

Оберемо для побудови контрольні точки, через які проведемо плавну криву на координатної площині.

\begin{array}{l} tg 0 = 0 \\ tg \frac{π}{6} = \frac{\sqrt{3}}{3} \\ tg \frac{π}{4} = 1 \\ tg \frac{π}{3} = \sqrt{3} \end{array}

Потім, відобразивши її симетрично відносно початку координат, отримаємо графік на інтервалі

(- \frac{π}{2}; \frac{π}{2})

Використовуючи періодичність, будуємо графік функції \(y = tg\) \(x\) на всій області визначення.
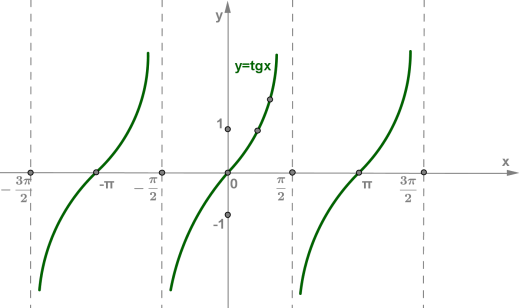
Графік функції \(y = tg\) \(x\) називають тангенсоїдою.

Головною гілкою графіка функції \(y = tg\) \(x\) називають гілку, яка знаходиться в інтервалі