Функція y = arcctg x — урок. Алгебра, 10 клас.

Функція

y = ctg x

монотонна на кажному з наступних інтервалів:

(- π; 0), (0; π), (π; 2 π)

і т.д.

Отже, на кожному із зазначених проміжків функція

y = ctg x

має обернену функцію.

Це різні обернені функції, але вибирають функцію, обернену до функції

y = ctg x

, де

x \in (0; π)

Її позначають

x = arcctg y

. Помінявши, як зазвичай,

x

y

місцями, отримаємо

y = arcctg x

, тобто функцію, обернену до функції

y = ctg x

, де

x \in (0; π)

Тому, графік функції

y = arcctg x

можна отримати з графіку функції

y = ctg x

x \in (0; π)

за допомогою перетворення симетрії відносно прямої

y = x

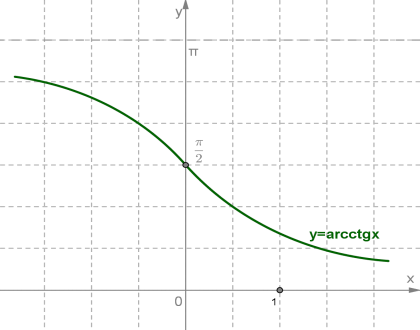
Властивості функції

y = arcctg x

D (f) = (- \infty; + \infty)

E (f) = (0; π)

3. Функція не є ні парною, ні непарною, оскільки графік функції не симетричний ні відносно початку координат, ні відносно осі

y

4. Функція спадає.

5. Функція безперервна.

arcctg a

- це таке число з інтервала

(0; π)

, котангенс якого дорівнює

a

Отже,

\begin{array}{l} arcctg a = t \Leftrightarrow \{\begin{cases} ctg t = a, \\ 0 < t < π; \end{cases} \\ ctg (arcctg a) = a \end{array}

Для арккотангенса має місце співвідношення, аналогічне для арккосинуса

arcctg (- a) = π - arcctg a

Знайшли помилку?

4. Функція y = arcctg x