За означенням арктангенса числа для кожного дійсного визначене одне число
Тим самим на всій числовій прямій визначена функція
Ця функція є оберненою до функції
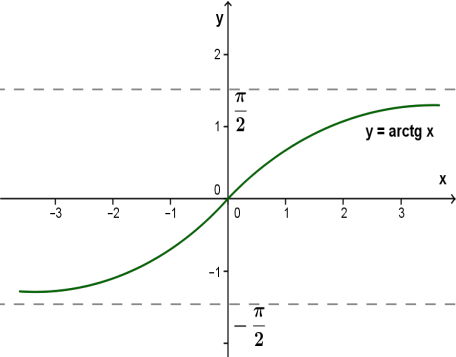
Графік функції
Основні властивості функції
1. Область визначення - множина всіх дійсних чисел
2. Множина значень - інтервал
3. Функція зростає.
4. Функція є непарною, оскільки
Функції називаються оберненими тригонометричними функціями.
