Функція при є непарною і періодичною з періодом .
Міркуючи аналогічно, як при побудові графіка функції \(y = tg\) \(x\), можна побудувати графік функції \(y=ctg\) \(x\).
Графік функції \(y=ctg\) \(x\), як і графік функції \(y = tg\) \(x\), називають тангенсоїдою.
Головною гілкою графіка функції \(y=ctg\) \(x\) називають гілку від \(x=0\) до \(x=\) .
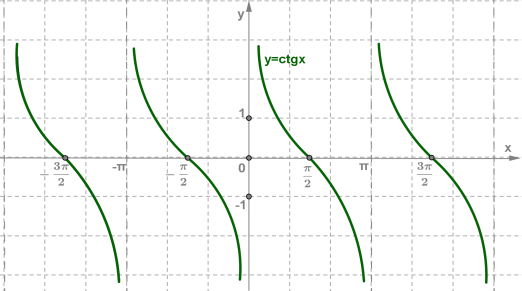
Властивості функції
1. Область визначення - множина всіх дійсних чисел
2. Множина значень - множина всіх дійсних чисел
3. Функція періодична з періодом
4. Функція непарна
5. Функція приймає:
- значення \(0\), при
- додатні значення на інтервалах
- від'ємні значення на інтервалах
6. Функція спадає на інтервалах