Дуже багато подій у нашому житті є наслідком спільного впливу великої кількості дрібних чинників.
Наприклад, час у дорозі на роботу залежить від заторів, світлофорів, пішоходів, і т. д. Усі ці чинники, накладаючись один на одного, і визначають час, витрачений на дорогу.
Але якщо постійно їздити на роботу, виробляється певний середній час. Така стійкість до сильних відхилень від середнього пов'язана з тим, що серед усієї множини незалежно від діючих дрібних факторів будуть існувати як фактори, що зменшують час у дорозі, так і фактори, що збільшують цей час.
Зменшувальні та підсилювальні фактори взаємно погашають один одного, тому сумарне відхилення від середнього невелике.
При цьому надзвичайно важливі дві речі:
\(1.\) Усі діючі фактори не повинні бути сильними.
\(2.\) Усі
діючі фактори повинні бути незалежними.
Математичним формулюванням цього принципу є закон великих чисел.
Для кожного додатного числа \(r\) при необмеженому збільшенні числа \(n\) незалежних повторень випробування з двома наслідками ймовірностей того, що частота \(k/n\) появи «успіху» відрізняється менш ніж на \(r\) від ймовірності \(p\) «успіху» в одному окремому випробуванні, наближається до одиниці.
Тобто середнє арифметичне багатьох незалежних випадкових величин зводиться до певного значення при збільшенні числа цих величин.
Механізм цього явища базується на тому, що відхилення вправо і вліво взаємно погашаються. Саме на цьому принципі засновано те, що багаторазове повторення одного й того самого призводить до майже передбачуваного результату.
Існує спосіб наближених обчислень ймовірності настання \(k\) «успіхів» в \(n\) незалежних повтореннях експерименту за допомогою гаусової функції.
Для гаусової функції є докладні таблиці її значень. Ці таблиці складені для значень аргументу \(x\) із кроком \(0,01.\)
Опишемо спосіб використання гаусової кривої для наближених обчислень у теоремі Бернуллі.
Алгоритм використання функції у наближених обчисленнях.
Для обчислення ймовірності потрібно:
- перевірити правильність нерівності \(npq >10;\)
- обчислити за формулою \(;\)
- за таблицею значень гаусової функції обчислити \(;\)
- попередній результат поділити на \(.\)
Ймовірності , як правило, дуже малі. Тому при великому числі \(n\) у схемі Бернуллі для числа \(k\) «успіхів» встановлюють не одне точне значення, а деякі рамки, в межах яких дозволено змінюватися числу \(k.\)
Ймовірність того, що число «успіхів» \(k\) в \(n\) випробуваннях Бернуллі знаходиться в межах від до позначають так:
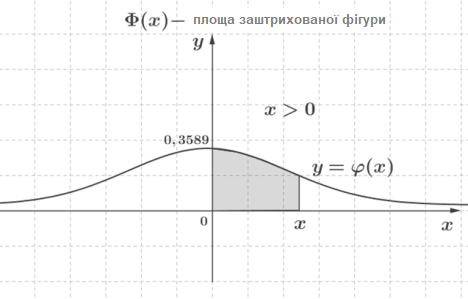
Графік функції \(:\)
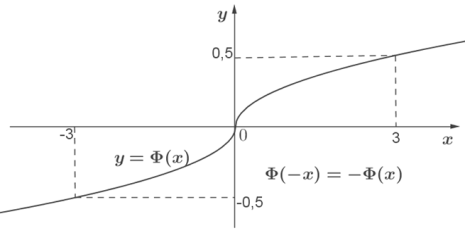
Алгоритм використання функції \(y= Ф(x)\) в наближених обчисленнях:
- перевірити правильність нерівності \(npq ≥ 10;\)
- обчислити і за формулами:
- за таблицею обчислити значення і \(;\)
- знайти різницю \(.\)
