В основі об'єднання ймовірності та статистики лежать два чудові факти. Один із них — явище статистичної стійкості. Другий полягає в тому, що в багатьох різних за своєю природою статистичних спостереженнях статистична стійкість може бути описана за допомогою однієї-єдиної функції.
Ця функція введена великим німецьким математиком Карлом Гаусом \((1777—1855).\) Вона задається досить складною формулою:
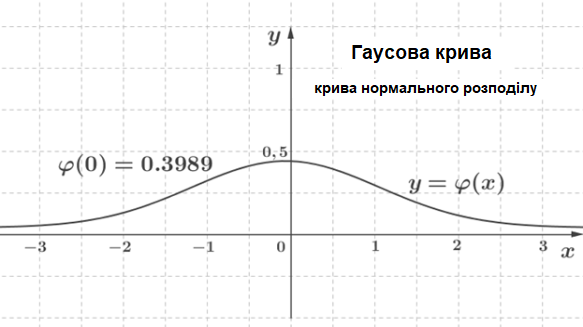
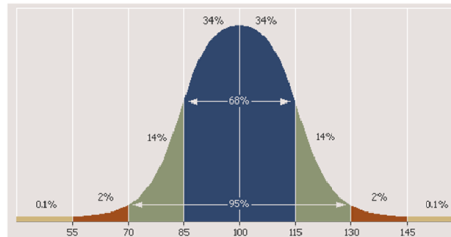
Якщо оцінити площу під кривою Гауса на відрізку \(,\) то вийде понад \(0,99,\) тобто більш ніж усієї площі.
Гістограми розподілу великого обсягу інформації незамінні у випадках, коли ряд даних складається з дуже великої кількості чисел. Якщо ширина вертикальних стовпців гістограми досить мала, а основи стовпців в об'єднанні дають деякий проміжок, то сама гістограма схожа на графік деякої неперервної функції, заданої на цьому проміжку. Іноді таку функцію називають вирівнюючою функцією.
Графіки вирівнюючих функцій гістограми схожі один на одного. Всі ці криві розподілу утворюються із кривої Гауса. Її часто називають кривою нормального розподілу.
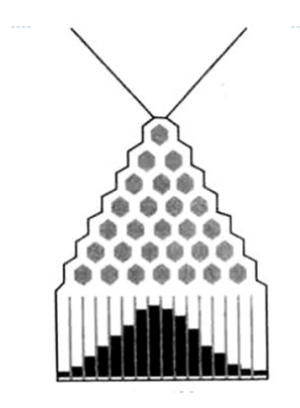
Для наочної демонстрації для гаусового закону розподілу іноді використовують спеціальний пристрій — дошку Гальтона (за іменем винахідника). У ньому однакові кульки, які сиплються зверху, розподіляються по сходинках між правильними шестикутниками і в результаті потрапляють на горизонтальну поверхню, утворюючи картинку, схожу на «підграфік» кривої Гауса.