Площа фігури, обмеженої графіками двох функцій і прямими \(x=a\) та \(x=b\)
Якщо на заданому відрізку неперервні функції і мають таку властивість, що для всіх , то
.
Приклад:
Визначимо площу фігури, обмеженої лініями (1) та (2).
Виконаємо побудову та визначимо асциси точок перетину:
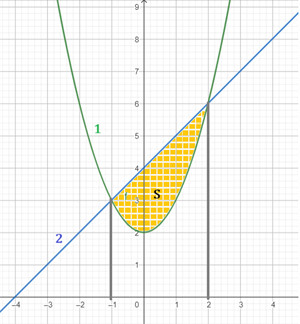
Тоді за формулою, маємо:
Обчислення об'ємів тіл
Якщо криволінійну трапецію, обмежену графіком неперервної та невід'ємної на відрізку функції \(f(x)\) і прямими \(x=a\) та \(x=b\) обертати навколо осі \(Ox\), то одержимо тіло, об'єм якого можна обчислити за формулою .
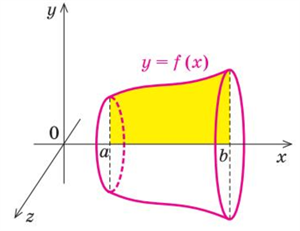
Також, якщо тіло обмежене двома перпендикулярними до осі \(Ox\) площинами, що проходять через точки \(x=a\) та \(x=b\), то , де \(S(x)\) — площа перерізу тіла площиною, що проходить точкою і перепендикулярно до осі \(Ox\).
Джерела:
Математика ( Алгебра і початки аналізу та геометрія/рівень стандарту): підр. для 11 кл. закл. заг. сер. освіти/ Є.П. Нелін, О.Є. Долгова. — Харків: Вид-во "Ранок". 2019.
Алгебра. 11-й клас: підручн. для ЗОНЗ: академ. рівень. профільний рів. Нелін, Долгова. — Вид. "Гімназія". — 2011 рік.