Для графічного розв'язання рівняння потрібно побудувати графіки функцій \(y=f(x)\) і \(y=g(x),\) а потім знайти точки їх перетину.
Коренями рівняння є абсциси цих точок.
Цей метод дозволяє визначити число коренів рівняння, вгадати значення кореня, знайти наближені, а іноді й точні значення коренів.
У деяких випадках побудову графіків функцій можна замінити посиланням на будь-які властивості функцій.
Якщо, наприклад, одна з функцій \(y=f(x),\) \(y=g(x)\) зростає, а інша спадає, то рівняння або не має коренів, або має один корінь (який іноді можна вгадати).
Якщо на проміжку \(X\) найбільше значення однієї з функцій \(y=f(x),\) \(y=g(x)\) дорівнює \(A\) і найменше значення іншої функції також дорівнює \(A,\) то рівняння на проміжку \(X\) рівносильне системі рівнянь:
Приклад:
Завдання 1. Розв'яжи рівняння:
Розв'язання
Побудуємо графіки функцій і на одній координатній площині.
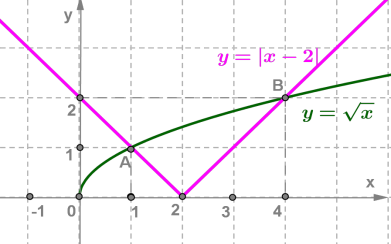
Ці графіки перетинаються в точках \(A(1;1)\) і \(B(4;2).\) Отже, рівняння має два корені:
Відповідь: \(1;4\)
Завдання 2. Розв'яжи рівняння:
Завдання 2. Розв'яжи рівняння:
Розв'язання
Перетворимо рівняння до вигляду \(.\) Розв'язання даного рівняння не потребує побудови графіків, якщо зауважити, що функція зростає, а функція \(y=42-5x\) — спадає.
Отже, рівняння має тільки один корінь. Це \(x=2.\) Дійсно, перевіривши \(,\) отримаємо правильну числову рівність.
Отже, рівняння має тільки один корінь. Це \(x=2.\) Дійсно, перевіривши \(,\) отримаємо правильну числову рівність.
Відповідь: \(2\)
