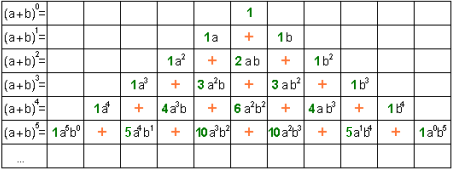
Біноміальна формула Ньютона — урок. Алгебра, 11 клас.

Біноміальна формула Ньютона:

\begin{array}{l} {(a + b)}^{n} = \\ = C_{n}^{0} a^{n} b^{0} + C_{n}^{1} a^{n - 1} b^{1} + C_{n}^{2} a^{n - 2} b^{2} + C_{n}^{3} a^{n - 3} b^{3} + ... + C_{n}^{k} a^{n - k} b^{k} + C_{n}^{n - 1} a^{1} b^{n - 1} + C_{n}^{n} a^{0} b^{n} \end{array}

Права частина формули називається розкладом степеня бінома.

C_{n}^{k}

називається біноміальними коефіцієнтами, а всі складові — членами бінома.

Біноміальні коефіцієнти — це ті числа, які складають трикутник Паскаля.

Сума біноміальних коефіцієнтів дорівнює

2^{n}

\(.\)

\begin{array}{l} {(a + b)}^{0} = 1 \\ {(a + b)}^{1} = 1 \cdot a + 1 \cdot b \\ {(a + b)}^{2} = 1 a^{2} + 2 ab + 1 b^{2} \\ {(a + b)}^{3} = 1 a^{3} + 3 a^{2} b + 3 {ab}^{2} + 1 b^{3} \\ {(a + b)}^{4} = 1 a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 {ab}^{3} + 1 b^{4} \end{array}

\begin{array}{l} C_{0}^{0} = 1 \\ C_{n}^{n} = 1 \\ C_{n}^{1} = n \end{array}

Приклад:

\(1.\) Напиши розклад степеня бінома.

\begin{array}{l} {(x - 2 y)}^{6} = {(x + (- 2 y))}^{6} = \\ = x^{6} + {6 x}^{5} (- 2 y) + 15 x^{4} {(- 2 y)}^{2} + 20 x^{3} {(- 2 y)}^{3} + 15 x^{2} {(- 2 y)}^{4} + \\ + 6 x {(- 2 y)}^{5} + {(- 2 y)}^{6} = \\ = x^{6} - {12 x}^{5} y + 60 x^{4} y^{2} - 160 x^{3} y^{3} + 240 x^{2} y^{4} - {192 xy}^{5} + {64 y}^{6} \end{array}

\(2.\) Обчисли середній член розкладу

{(3 a + b)}^{6}

\(.\)

Розв'язання

У розкладі \(6 + 1 = 7\) членів, отже, середній член — четвертий.

T_{4} = T_{3 + 1} = C_{6}^{3} {(3 a)}^{6 - 3} \cdot b^{3} = \frac{6 \cdot 5 \cdot 4}{3 \cdot 2 \cdot 1} \cdot 27 a^{3} b^{3} = 540 a^{3} b^{3}

\(3.\) Обчисли член розкладу

{(x^{2} + \frac{1}{x})}^{12}

\(,\) який містить

x^{3}

\(.\)

Розв'язання

T_{k + 1} = C_{12}^{k} {(x^{2})}^{12 - k} \cdot {(x^{- 1})}^{k} = C_{12}^{k} x^{24 - 2 k} \cdot x^{- k} = C_{12}^{k} x^{24 - 3 k}

Якщо член містить

x^{3}

\(,\) то

x^{24 - 3 k} = x^{3}

\(;\)

24 - 3 k = 3

\(;\)

k = \frac{24 - 3}{3} = 7

Отже, це

k + 1 = 7 + 1 = 8 .

T_{8} = C_{12}^{7} x^{3} = C_{12}^{5} x^{3} = \frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \cdot x^{3} = \frac{95040}{120} \cdot x^{3} = 792 x^{3}

Відповідь: \(8\) член розкладу дорівнює

792 x^{3}

\(.\)

«Біном» із грецької мови перекладається як «двочлен».

Знайшли помилку?

2. Біноміальна формула Ньютона