Метою збору даних є знання про об'єкт дослідження — виявлення корисної інформації, знайдення висновків, прийняття рішень.
Вивчення зібраної інформації може мати багато підходів, реалізовуватися за допомогою різних інструментів — в тому числі математичних, статистичних, за допомогою засобів візуалізації, але головне завдання його — аналіз зібраних даних. Цим питанням присвячений окремий розділ математики.
Статистика (від латинського status — стан) — це наука про отримання, оброблення й аналіз кількісних даних, які характеризують масові явища в житті.
Математична статистика — розділ математики, який вивчає математичні методи обробки статистичних даних та їх використання для наукових і практичних спостережень.
Статистичні дані — сукупність чисел, які дають кількісну характеристику ознак певних об'єктів та явищ, що нас цікавлять. Кількість об'єктів сукупності називають обсягом сукупності.
Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіаційним рядом. Зібрану інформацію (сукупність даних) зручно подавати у вигляді таблиць, графіків, діаграм (гістограм).
Діаграма — це графічне представлення даних, у якому числові дані подано геометричними фігурами.
Діаграми особливо корисні для спрощення складних наборів даних, щоб розкрити форму даних. Основними типами діаграм є кругова (секторна) діаграма, стовпчаста діаграма і лінійчата (графік).
Кругова (секторна) діаграма наочно показує співвідношення між частинами в цілому. Даний вид діаграм найкраще підходять для складання графіків даних, які становлять відсоток від цілого.
В статистиці стовпчасту діаграму називають гістограмою. Дані візуалізації найкраще використовувати для відображення інформації по елементах, що відрізняються одне від одного.
Частоти — числа, які показують, скільки разів повторюється кожне значення ознаки сукупності.
Відношення частоти до обсягу вибірки називають відносною частотою.
Приклад:
Дано вибірку оцінок класу: \(4\); \(4\); \(5\); \(9\); \(5\); \(3\); \(9\); \(9\); \(8\); \(5\); \(8\); \(9\); \(8\); \(8\); \(10\); \(9\).
Складемо таблицю чатот за даними вибірки та знайдемо відносну частоту варіантів.
— варіанти вибірки;
\(3\); \(4\); \(5\); \(8\); \(9\); \(10\) варіаційний ряд.
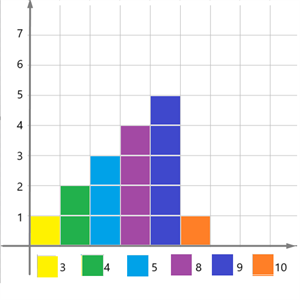
Частота варіанти дорівнює \(1\); дорівнює \(2\); — \(3\); — \(4\); — \(5\); — \(1\).
| Оцінка | \(3\) | \(4\) | \(5\) | \(8\) | \(9\) | \(10\) |
| Частота | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(1\) |
Відносна частота є відношенням частоти до загальної кількості, отже частоти варіантів:
Для того щоб подати отримані дані наочно, побудуємо на координатній площині стовпчасту діаграму.
Джерела:
Підручник для 7 класу "Алгебра" авт. Біляніна О.Я., Семчук А.Р .- 2024
