Функцію, зокрема її графік, можна зустріти скрізь! Все що програмується, комп'ютерні системи, розрахунки доходів, податки, прогнози росту тощо.
Вже відомо, що лінійні функції відіграють ключову роль у розумінні та моделюванні різноманітних явищ у реальному світі та широко використовуються в різних галузях життя і науки через їхню простоту та математичну чіткість.
На практиці досить часто викоритовуються прилади з автоматичною реєстрацією того чи іншого процесу, що викреслють графіки відповідних функціональних залежностей. Кожний вчений уміє не лише "читати" дані графіки, а ще й будувати їх самостійно, без використання приладів.
Зверни увагу!
Функції, в тому числі й лінійні, є невід'ємною складовою для вирішення практичних завдань.
Прочитаймо графік функції, який відображає кількість осіб деякої територіальної громади, які взимку минулого року хворіли на грип.
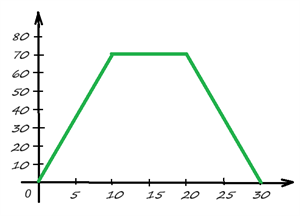
За графіком видно, що він має три частини відслідковування етапів процесу.
На першому етапі ми бачимо зростання кількості захворюваних на грип. Коли відбулось десятого дня досягнення піку, ситуація протрималась деякий час без змін.
На третьому етапі кількість хворих почала зменшуватись, й досягла на тридцятий день нульового значення.
Як відомо, прямокутну систему координат зручно використовувати для побудови графіків залежності двох величин, таких як графік залежності висоти дерева від його віку, маси тіла людини від віку чи температури повітря від часу дня та ін.
Зверни увагу!
Для більш точної побудови графіків їх креслять на міліметровому папері.
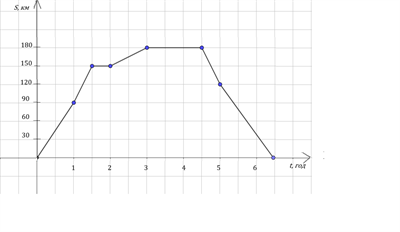
На практиці часто трапляються ступінчасті графіки, їх використовують у медицині, економіці, соціології тощо. Це лінійні функції, областю визначення яких є відрізок, а графіком — ламана.
Наприклад графік залежності подоланого шляху від часу.