Пригадай, що для функції характерно, що кожному значенню аргумента відповідає єдине значення функції. Тобто за графіком завжди можна визначити, чи є він графіком саме функції.
За графіком функції можна визначити:
1. координату точки, яка належить графіку;
2. область визначення функції;
3. область значень функції;
4. точки перетину графіка із осями координат;
5. значення аргументу, при яких \(y>0\), й при яких \(y<0\).
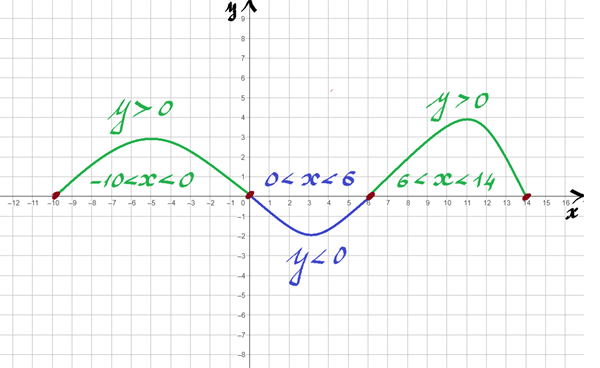
Зверни увагу!
Уміння визначати згадані властивості за графіком функції ще називають читанням графіка.
Розглянемо властивості функції за її графіком.
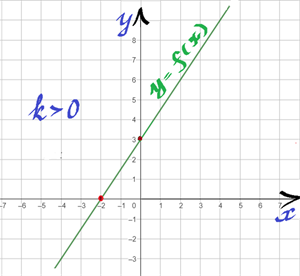
1. Область визначення функції: всі числа;
2. Область значень функції: всі числа;
3. Якщо \(x=0\), то \(y=3\), отже \((0;3)\) — точка перетину графіка з віссю \(Oy\);
4. Якщо \(y=0\), то \(x=-2\), отже \((-2;0)\) — точка перетину графіка з віссю \(Ox\);
5. Значення аргументу, при яких \(y>0\), тобто функція набуває додатних значень — \(x>-2\);
6. Значення аргументу при яких \(y<0\), тобто функція набуває від'ємних значень — \(x<-2\).
Властивості розміщення графіку лінійної функції у загальному випадку.
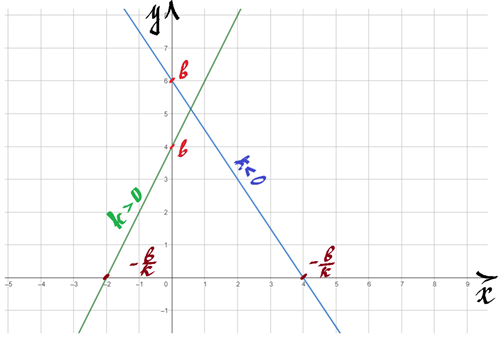
1. Область визначення функції: всі числа;
2. Область значень функції: всі числа;
3. Якщо \(x=0\), то \(y=b\), отже \((0;b)\) — точка перетину графіка з віссю \(Oy\);
4. Якщо \(y=0\), то , отже \((\)\(;0)\) — точка перетину графіка з віссю \(Ox\);
5. Функція набуває додатних значень, а саме \(y>0\), при , якщо \(k>0\), та , якщо \(k<0\).
6. Функція набуває від'ємних значень, тобто \(y<0\), при , якщо \(k>0\), та , якщо \(k<0\).
7. Кут нахилу графіка до додатної півосі \(Ox\) — гострий, якщо \(k<0\) та тупий при \(k<0\).
