Нагадаємо, що залежність однієї змінної від іншої називають функцією, якщо кожному значенню незалежної змінної за деяким правилом відповідає єдине значення залежної змінної.
Задавати функцію можна різними способами. Розглянемо чотири основні способи задання функції: словесний, табличний, графічний та аналітичний.
Словесний (описовий) спосіб полягає в тому, що правило, за яким одній змінній ставиться у відповідність інша, описують словами.
Прикладом може слугувати умова завдання.
Загальна вартість поїздки на таксі залежить від відстані. Задати функцією залежність вартості поїздки на таксі від довжини маршруту, якщо поїздка в межах двох кілометрів коштує 30 грн, а кожен додатковий км тарифікується по 10 грн.
Табличний спосіб полягає в тому, що відповідність між \(x\) та \(y\) задають таблично.
Подамо функцію описану вище (вартість поїздки на таксі) у вигляді таблиці.
| Відстань, \(x\) км | 1 | 2 | 3 | 4 | 5 | ... |
| Вартість, \(y\) грн | 30 | 30 | 40 | 50 | 60 | ... |
Аналітичний спосіб полягає в тому, що функцію задають за допомогою формули \(y = f(x)\), де \(f(x)\) — вираз зі змінною \(x\).
Повернемось знов до прикладу розрахунку вартості \(y\) (грн) послуги таксі залежно від відстані \(x\) (км) матиме вигляд \(y = 30 + 10(x-2)\).
Графічний спосіб полягає у поданні функції у вигляді графіку.
Графіком називають множину точок координатної площини, абсциси яких дорівнюють аргументу функції, а ординати відповідному значенню функції.
Задамо графік за прикладом розрахунку вартості поїздки на таксі (таблиця):
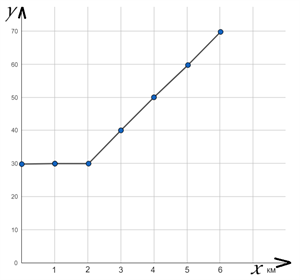
Визначення окремих характеристик функції за її графіком
За графіком можна одразу вказати, для яких значень аргументу значення функції додатні, для яких — від'ємні, для яких дорівнють нулю. Також, за графіком визначають область визначення на область значень функції.
Нулем функції називають таке значення аргументу, для якого значення функції дорівнює нулю.
Зрозуміло, що це асциси точок перетину графіка функції з віссю абсцис, бо в таких точках значення функції (ординати) — рівні нулю.
Графічний спосіб задання функції є зручним своєю наочністю, тому його часто використовують для відображення явищ, які відбуваються в навколишньому світі.
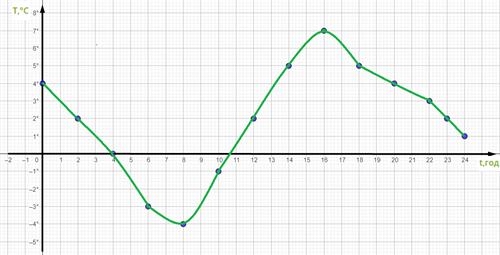
Наприклад, графік зміни температури повітря протягом доби.
Зверни увагу!
Щоб фігура, яку зображено на координатній площині була графіком деякої функції, необхідно, щоб кожна пряма, перпендикулярна до осі абсцис, перетинала фігуру не більше ніж в одній точці.
Джерела:
О. Біляніна "Алгебра 7 клас", 2024
