Взаємне розміщення графіків лінійних функцій

Виконуючи побудову графіків лінійних функцій, помічаємо, що прямі можуть перетинатися, можуть не перетинатися, тобто бути паралельними або збігатися.

Справедлива така теорема:

Нехай дано дві лінійні функції

y = k_{1} x + b_{1}

y = k_{2} x + b_{2}

Прямі, що є графіками заданих лінійних функцій:
1) паралельні, якщо

k_{1} = k_{2}; b_{1} \neq b_{2}

;

2) збігаються, якщо

k_{1} = k_{2}; b_{1} = b_{2}

;

3) перетинаються, якщо

k_{1} \neq k_{2}

Приклад:

1. Знайти точку перетину прямих:

y = 2 x - 3

y = 2 - 0,5 x

Для побудови графіка кожної лінійної функції складемо таблицю значень.

Для функції

y = 2 x - 3

маємо:

\(x\)	\(0\)	\(2\)
\(y\)	\(-3\)	\(1\)

Через отримані точки проведемо пряму

l_{1}

Для функції

y = 2 - 0,5 x

маємо:

\(x\)	\(0\)	\(2\)
\(y\)	\(2\)	\(1\)

Через отримані точки проведемо пряму

l_{2}

Прямі

l_{1}

l_{2}

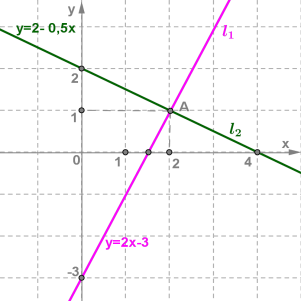
перетинаються в точці \(А(2;1)\).

2. Знайти точку перетину прямих:

y = - 3 x + 1

y = - 3 x + 5

У даних лінійних функцій однаковий кутовий коефіцієнт \(k = -3\), отже, прямі

y = - 3 x + 1

y = - 3 x + 5

будуть паралельні, тобто точки перетину в них немає.

3. Знайти точку перетину прямих:

y = 4 x + 7

y = - 2 x + 7

У даних лінійних функцій кутові коефіцієнти різні

k_{1} = 4

k_{2} = - 2

, отже, прямі перетинаються в одній точці.

Можна помітити, що обидві прямі проходять через точку \((0; 7)\).
Отже, точка \((0; 7)\) і є точкою перетину даних прямих.
Прямі

y = k_{1} x + b

y = k_{2} x + b

, де

k_{1} \neq k_{2}

, перетинаються в точці \((0; b)\).

Знайшли помилку?

1. Взаємне розміщення графіків лінійних функцій