Формули для розкладання на множники виразів виду aⁿ – bⁿ і aⁿ + bⁿ

Ти вже знайомий з формулами скороченного множення

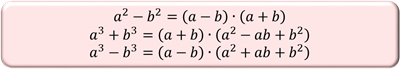
Якщо продовжити аналіз то отримуються наступні формули

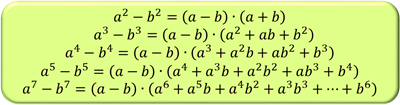
У даній структурі можна побачити чітку закономірність і відповідно записати загальну формулу

Складніше розкладати на множники суму \(n-x\) степенів.

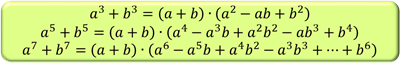
Загальну формулу можна запропонувати тільки для непарних степенів.

Дані розкладання застосовують для спрощення виразів, розв'язування рівнянь і визначення подільності.

Приклад:

№1 Спрости вираз

\begin{array}{l} \frac{a^{9} - b^{9}}{a^{8} + a^{7} b + a^{6} b^{2} + ... + b^{8}} = \\ \frac{(a - b) (a^{8} + a^{7} b + ... + b^{8})}{a^{8} + a^{7} b + a^{6} b^{2} + ... + b^{8}} = \\ = a - b \end{array}

Приклад:

№2 Знайди дільник виразу

\begin{array}{l} 7^{8} - 256 \\ 7^{8} - 256 = 7^{8} - 2^{8} = \\ = (7 - 2) \cdot \\ (7^{7} + 7^{6} \cdot 2 + 7^{5} \cdot 2^{2} + ... + 2^{7}) \\ = 5 \cdot (7^{7} + 7^{6} \cdot 2 + ... + 2^{7}) \end{array}

5 \cdot (7^{7} + 7^{6} \cdot 2 + ... + 2^{7})

\(5\)

\Rightarrow 7^{8} - 256

\(5\)

Відповідь: \(5\) — дільник заданого виразу

Приклад:

№3 Знайди корінь роівняння

125 + 25 x + 5 x^{2} + x^{3} = 0

Очевидно, що число \(5\) не може бути коренем рівняння, тоді вираз

x - 5 \neq 0

Домнож праву і ліву частини рівняння на вираз \(x - 5\)

\begin{array}{l} 5^{3} + 5^{2} x + 5 x^{2} + x^{3} = 0 \\ (x - 5) (x^{3} + ... + 5^{3}) = \\ = 0 \cdot (x - 5) \\ x^{4} - 5^{4} = 0 \\ x^{4} = 5^{4} \\ x = 5 або x = - 5 \end{array}

За визначеним раніше \(5\) сторонній корінь

Відповідь: \(x = -5\)

Знайшли помилку?

1. Формули для розкладання на множники виразів виду aⁿ – bⁿ і aⁿ + bⁿ