Пригадаємо, що аби розв'язати систему, потрібно знайти всі її розв'язки або встановити, що їх немає.
Завдання 1. Розв'язати систему рівнянь
Графіком рівняння є пряма.
Знайдемо дві пари значень змінних \(x\) та \(y,\) що задовольняють цьому рівнянню.
Знайдемо дві пари значень змінних \(x\) та \(y,\) що задовольняють цьому рівнянню.
| \(x\) | \(5\) | \(0\) |
| \(y\) | \(0\) | \(2,5\) |
Побудуємо на координатній площині \(xОy\) пряму \(,\) яка проходить через ці дві точки.
Графіком рівняння також є пряма.
Знайдемо дві пари значень змінних \(x\) та \(y,\) що задовольняють цьому рівнянню.
Знайдемо дві пари значень змінних \(x\) та \(y,\) що задовольняють цьому рівнянню.
| \(x\) | \(-1,5\) | \(2,5\) |
| \(y\) | \(0\) | \(-2\) |
Побудуємо на координатній площині \(xОy\) пряму \(,\) що проходить через ці дві точки.
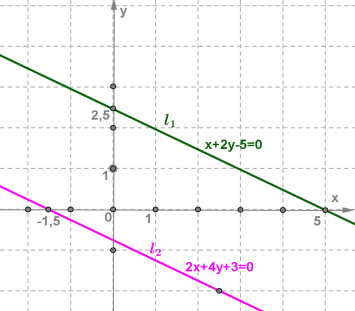
Прямі \(і\) паралельні. Отже, система не має розв'язків, оскільки немає точок, що задовольняють одночасно і першому, і другому рівнянню, тобто належать одночасно і першій, і другій із побудованих прямих.
Відповідь: система не має розв'язків.
Завдання 2. Розв'язати систему рівнянь:
Побудуємо графіки рівнянь системи, приведемо кожне рівняння до вигляду лінійної функції. Отримаємо з першого рівняння \(y = 2x - 5\) і з другого рівняння \(y = -2x + 7\).
Графіком рівняння \(y = 2x - 5\) є пряма.
Знайдемо дві пари значень змінних \(x\) та \(y,\) що задовольняють цьому рівнянню.
| \(x\) | \(0\) | \(3\) |
| \(y\) | \(-5\) | \(1\) |
Побудуємо на координатній площині \(xОy\) пряму \(,\) яка проходить через ці дві точки.
Графіком рівняння \(y =-2x +7\) також є пряма.
Графіком рівняння \(y =-2x +7\) також є пряма.
Знайдемо дві пари значень змінних \(x\) та \(y\), що задовільняють цьому рівнянню.
| \(x\) | \(0\) | \(1\) |
| \(y\) | \(7\) | \(5\) |
Побудуємо на координатній площині \(xОy\) пряму \(,\) що проходить через ці дві точки.
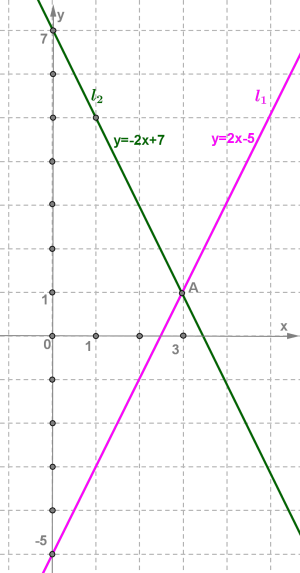
Прямі \(і\) перетинаються в точці \(A,\) координати якої — єдиний розв'язок даної системи.
Відповідь: \((3;1).\)
Для розв'язання цих двох прикладів застосовувався графічний метод розв'язання системи лінійних рівнянь.
Алгоритм розв'язування системи рівнянь графічно:
1. для кожного рівняння системи скласти таблицю значень \(x\) та \(y\).
2. побудувати графіки рівнянь системи в одній координатній площині;
3. знайти координати точки перетину графіків, або впевнитись, що таких немає (паралельні) або безліч (збігаються);
4. якщо координати точки перетину є цілими числами, виконати перевірку, інакше — визначити розв'язок наближено;
5. записати розв'язок у відповідь.
Отже, даний метод є наближеним, оскільки координати точки перетину за кресленням не завжди легко визначити. Але все-таки графічний метод розв'язання системи лінійних рівнянь дуже важливий, коли необхідно визначити кількість розв'язків.
Зверни увагу!
Застосовуючи його, можна дійти таких висновків, що система з двох лінійних рівняння з двома змінними \(x\) та \(y\)
\(1.\) Матиме єдиний розв'язок, якщо прямі, які є графіками рівнянь, будуть перетинатися в одній точці, а коефіцієнти при змінних не будуть пропорційними:
\(2.\)Не матиме розв'язків (система несумісна), якщо прямі будуть паралельні, а коефіцієнти при змінних будуть пропорційними, проте не пропорційні вільним членам:
\(3.\)Матиме нескінченну кількість розв'язків (система невизначена), прямі збігаються, а коефіцієнти при всіх змінних будуть пропорційними:
