Рівняння виду , де \(a, b, c\) — числа (коефіцієнти), \(x\) та \(y\) - змінні, називається лінійним рівнянням з двома змінними .
Розв'язком рівняння називають будь-яку пару чисел (\(x\);\(y\)), яка задовольняє це рівняння, тобто перетворює рівність зі змінними на правильну числову рівність.
Приклад:
Зобразити розв'язок лінійного рівняння з двома змінними точками у координатній площині \(xOy\).
Підберемо кілька розв'язків заданого рівняння, тобто кілька пар чисел, які задовольняють рівняння: \((3, 0), (2; 1), (1, 2), (0, 3), (4; -1)\).
Побудуємо у координатній площині \(xOy \) ці точки.
Усі вони лежать на одній прямій \(t\).
Усі вони лежать на одній прямій \(t\).
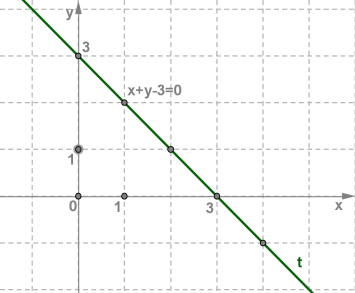
Пряма \(t\) є графіком рівняння , або
пряма \(t\) є геометричною моделлю цього рівняння.
пряма \(t\) є геометричною моделлю цього рівняння.
Отже, якщо пара чисел (\(x\); \(y\)) задовольняє рівняння
, то точка \(М\)(\(x\);\(y\)) належить прямій \(t\).
І навпаки, якщо точка \(М\)(\(x\);\(y\)) належить прямій \(t\), то пара чисел (\(x\);\(y\)) задовольняє рівняння .
Справедливою є така теорема:
Якщо хоча б один з коефіцієнтів \(a, b\) лінійного рівняння відмінний від нуля, то графіком рівняння служить пряма лінія.
Алгоритм побудови графіка рівняння , де
1. Надати змінній \(x\) конкретне значення ;
з рівняння знайти відповідне значення .
2. Надати змінній \(x\) інше значення ;
з рівняння знайти відповідне значення .
3. Побудувати на координатній площині \(xOy\) точки:
4. Провести через ці дві точки пряму — вона і буде графіком рівняння
Приклад:
Побудувати графік рівняння .
Будемо діяти за алгоритмом. 1. Нехай \(x = 0\), тоді отримаємо:
2. Нехай \(y = 0\), тоді отримаємо:
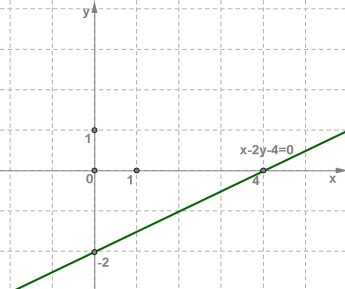
3. Побудуємо на координатній площині \(xOy\) отримані точки:
\((0;-2)\) та \((4;0)\)
4. Проведемо через ці точки пряму.

Вона і буде графіком лінійного рівняння .
