Множення одночленів
Під час множення одночленів використовують властивості множення та правило множення степенів з однаковими основами:
.
При множенні одночленів:
— перемножуються коефіцієнти одночленів;
— показники степенів з однаковими основами додаються;
— перемножуються коефіцієнти одночленів;
— показники степенів з однаковими основами додаються;
— добутком будь-яких одночленів є одночлен, який подають у стандартному вигляді.
Можна множити два, три і більше одночлени.
Щоб помножити одночлени потрібно запам’ятати, що коефіцієнти та буквені частини перемножуються, при цьому показники степенів однакових змінних додаються.
Приклад:
Значення виразу  дорівнює ...
дорівнює ...
 дорівнює ...
дорівнює ...1) Щоб вираз був легшим, множники міняють місцями:
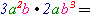
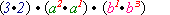 =
=2) Перемножуються коефіцієнти одночленів, показники степенів з однаковими основами додаються:
= 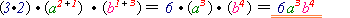 .
.
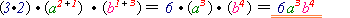 .
.Приклад:
Значення виразу 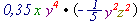 дорівнює...
дорівнює...
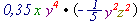 дорівнює...
дорівнює...1) Щоб вираз був легшим, множники міняють місцями:
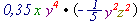 =
= 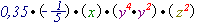 =
=2) Коефіцієнт одночлена можна записати як десятковий дріб \(–0,20\):
= 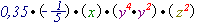 =
= 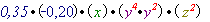 .
.
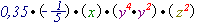 =
= 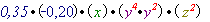 .
.3) Перемножуються коефіцієнти одночленів, показники степенів з однаковими основами додаються:
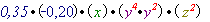 =
= 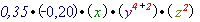 =
=.
Піднесення одночленів до степеня
Під час піднесення одночлена до степеня використовуютьчя властивості степенів.
При піднесенні одночлена до степеня:
— кожен множник одночлена підноситься до степеня окремо;
— показники змінних множників одночлена (букви) перемножаються на показник степеня, до якого треба піднести одночлен.
— кожен множник одночлена підноситься до степеня окремо;
— показники змінних множників одночлена (букви) перемножаються на показник степеня, до якого треба піднести одночлен.
Підносимо до степеня одночлен 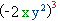 , отримуємо:
, отримуємо:
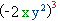 , отримуємо:
, отримуємо:1) Одночлен розкладемо на множники.
Зверни увагу!
Запам'ятай: якщо степінь не вказаний, він дорівнює \(1\)
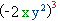 =
= 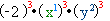 .
.2) Кожен множник підноситься до степеня окремо.
Зверни увагу!
Показники степеня змінних множиться на показник степеня, до якого підносимо одночлен.
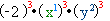 =
= 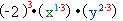 =
= 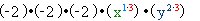 .
.3) Підносячи від’ємний коефіцієнт до непарного степеня, отримуємо від’ємний результат:
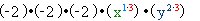 .
.